Coeficiente binomial

Definición

Sea (a+b)ⁿ = C₀aⁿb⁰+C₁a^n-1b¹+C₂a^n-2b²+...+C_n-1a¹b^n-1+C_na⁰bⁿ se llama coeficiente binomial n, r; al coeficiente C_r de la expresión antes vista, donde n es el exponente del binomio a+b y se representa ó . Esta forma de definición se debe a Isaac Newton y es equivalente al llamado teorema del binomio o teorema de Newton.

También el coeficiente binomial de n, r coincide con la cantidad de r-combinaciones sin repetición de los elementos de un n-conjunto dado por el resultado:

donde P_r,n es la cantidad de r-permutaciones en un n-conjunto.

Propiedades

El coeficiente binomial presenta una serie de propiedades bien conocidas como son:

1. 
2. 
3. (Fórmula recursiva aditiva del coeficiente binomial).
4. (Identidad de simetría del coeficiente binomial).
5. (Cantidad de subconjuntos en un conjunto de n elementos).

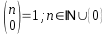
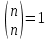
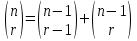
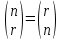
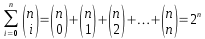
Las cuatro primeras sirven para la contrucción recurrente del coeficiente binomial. En lenguaje de programación Python sería:

def C(n,k):
    '''(int, int)--> int. Devuelve el valor del coeficiente binomial de n, k.'''
    if n==k or k==0:
        return 1
    if k>n:
        return 0
    if k > n/2:
        return C(n,n-k)
    return C(n-1,k-1) + C(n-1,k)

La quinta es la formulación combinatoria del famoso resultado de la Teoría de Conjuntos: si |A|=n entonces |P(A)|=2ⁿ.

def Triangulo_Pascal(n):
    '''(int)--> list. Devuelve una lista cuyos elementos son
listas que representan las filas del Triangulo de Pascal.'''
    TP = []
    for i in range(n+1):
        F = [C(i, 0)]
        for j in range(1,i+1):
            F.append(C(i,j))
        TP.append(F)
    return TP

Antecedentes

Las formulaciones tanto algebraicas como combinatorias e incluso la forma misma de los números de los coeficientes binomiales dispuestos triangularmente eran conocidos desde la antiguedad mucho antes de quedar formalizadas en 1654, por Blaise Pascal en su "Traité du triangle arithmétique" (trad.: "Tradado del triángulo aritmético"), que constituyó uno de los primeros documentos sobre Análisis Combinatorio y Probabilístico.

Hay referentes escritos de la India y Persia donde matemáticos como Al-Karaji y Omar Jayyam exponen sus consideraciones y análisis al respecto cinco siglos antes que Pascal. En 1303 el chino Yang Hui describe su forma, valores e importancia, haciendo que en su país se nombrara como Triángulo de Yanghui. No obstante el uso se remonta atrás en el tiempo.

Fuentes

1. K. Ribnikov. Análisis Combinatorio. Editorial Mir. Moscú, 1988.
2. K. Ribnikov. Historia de las Matemáticas. Editorial Mir. Moscú, 1987.
3. I. Bronshtein, K. Semendiaev. Manual de Matemáticas para ingenieros y estudiantes. 2da Edición. Editorial Mir. Moscú, 1973.
4. Colectivo de Autores. Matemática 12 grado. Tomo 1. Editorial Pueblo y Educación. La Habana, 1989.
5. Página del Coeficiente binomial en Wikipedia.
6. Triángulo de Pascal en Wikipedia.