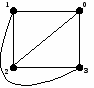
Grafo planar
| ||||||
Esta caracterísica de algunos grafos surgió evidentemente en problemas de entretenimiento pero presenta gran utilidad en varias ramas y terrenos técnicos como la construcción de circuitos en una sola placa, sin necesidad de recurrir a conectores externos.
Definición
Un grafo G=<V,A> se dice plano o planar si y solo si satisface cualquiera de las siguientes propiedades:
- Puede graficarse de una manera que ninguna arista se cruce con otra.
- Teorema de Kuratowski: G no contiene ningún subgrafo homeomorfo de los llamados grafos de Kuratowski: K5 y K3,3.
Orígenes e implicaciones
Es difícil saber si el problema base de representación de grafos planos surgió en la práctica o como juego mental, lo que sí es cierto que tiene aplicaciones que escapan al papel y las teorías.
Uno de los orígenes como problema mental podría estar en el caso del Problema de las 3 casas y los 3 pozos:
Gráficos
Tras unir de manera trivial las casas y los pozos queda:
La solución a este problema no existe porque el grafo resultante es isomorfo o mejor idéntico a K3,3 que como ya se sabe siempre tendrá un par de aristas (caminos en el problema) que se crucen.
Problemas similares pudieron tener los especialistas en topología o los constructores de placas de circuitos electrónicos que quisieran saber de antemano si tendrían que recurrir a conectores externos como cables o puentes de metal.
El problema de la definición radica en que para grafos pequeños es relativamente fácil detectar si son homeomorfos o derivaciones constructivas de los grafos de Kuratowski, pero en las placas de circuitos puede haber gran cantidad de puntos a unir, dificultándose la determinación rápida de su planaridad.
Fuentes
- K. Ribnikov. Análisis Combinatorio. Editorial Mir. Moscú, 1988. Páginas 17-23.
- Grafo plano. Disponible en "es.wikipedia.org". Consultado 29 de noviembre de 2011.
- Teoría de grafos.Disponible en "es.wikipedia.org". Consultado 29 de noviembre de 2011.