Grafo simple

Definición

En los textos difiere el concepto entre estas dos versiones:

Sea un grafo G=<V,A> se dice que es un grafo simple si y solo si se cumple una de estas propiedades:

1. Para todo par de vértices x,y de V y el conjunto , |S_x,y|<2.
2. Para todo par de vértices x,y de V y el conjunto , |S_x,y|<2 y si x=y, |S_x,y|=0.

Como se puede apreciar, la diferencia entre un caso y el otro radica que en el segundo se incluye el hecho de que el concepto incluye a los grafos sin lazos. Ya se mencionó que la definición suele usarse de una u otra forma, pero a los efectos de las definiciones hechas en esta enciclopedia se tomará la segunda: grafo sin aristas múltiples ni lazos.

Consecuencias y ejemplos.

En la Teoría de grafos el concepto de grafo simple es muy recurrido en la definición de otros entes, como los de grafos completos, grafos bipartidos completos, arboles y otros más.

Las definiciones aportan una formalización lógica a hechos abstractos o naturales, muchas veces ya definidos de forma intuitiva. En este caso la imagen de grafo simple es fácil de reconocer ante otro que no lo es; bien por la presencia de lazos o de más de una arista entre los pares de vértices.

Grafo simple	No simple	No simple	No simple
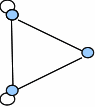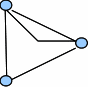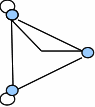Satisface la definición	Tiene lazos	Tiene multiaristas	Lazos y multiaristas

Otro detalle a tener en cuenta es que como consecuencia de la formalización de los grafos simples sus matrices de adyacencia tienen todos sus elementos a no más de 1 y que la diagonal principal estará a 0.

El siguiente fragmento de código Python permite comprobar si un grafo dado como un par de secuencias de vértices y aristas es simple:

def es_simple(V, A):
    for v1,v2 in A:
        if v1==v2:
            return False
        c = 0
        for a in A:
            if set((v1,v2)) == set(a):
                if c:
                    return False
                else:
                    c += 1                
    return True