Jerarquía de Chomsky

Jerarquía de Chomsky

Concepto:	Sistema de definiciones que permite clasificar de 4 formas posibles los lenguajes formales ideado por Noam Chomsky.

Jerarquía de Chomsky. En Lingüística, Matemáticas e Informática dícese del sistema jerárquico de definiciones, ideado por Noam Chomsky en 1956 en el MIT para clasificar de manera matemática los lenguajes formales en cuatro categorías enumeradas de 0 a 3 y los mecanismos formalizadores como gramáticas formales, expresiones y autómatas para reconocer cada tipo.

También se conoce bajo el nombre de Clasificación de Chomsky o Jerarquía matemática de los lenguajes.

La Jerarquía de Chomsky.

Sea un lenguaje L definido por al menos una gramática G que cumple:

Si todas las producciones de G tienen la forma ó donde A y B son simbolos no terminales y x es un terminal; entonces G se dice que es una gramática regular y L es un lenguaje regular o de tipo 3.
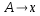
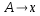
Si todas las producciones de G tienen la forma donde x es una combinación de símbolos terminales y no terminales, entonces G se dice que es una gramática libre de contexto y L es un lenguaje libre de contexto o de tipo 2.
De ser las producciones de G de la forma donde A es un símbolo no terminal cualquiera, x, y, y z son combinaciones de terminales y no terminales, tales que x e y pueden ser cadenas vacías; entonces se dice que G es una gramática dependiente del contexto y L es un lenguaje dependiente del contexto o lenguaje de tipo 1.
Si ninguna de las gramáticas de L cumple las propiedades anteriores entonces se dice que es un lenguaje sin restricciones, recursivamente enumerable o de tipo 0.

Desde el punto de vista conjuntual la jerarquía de Chomsky funciona como se ve en al gráfico:

.

De manera que todos los lenguajes de tipo 3 (LR) son también de tipo 2 (LLC) y los LLC son de tipo 1 (LDC) son de tipo 0 (LSR ó LRE).

Consecuencias.

La jerarquía de Chomsky no solo aporta un ordenamiento conjuntual de los lenguajes, sino que proporciona un mecanismo de clasificación basado en características relacionadas con las formas gramaticales mínimas de cada lenguaje en particular así como decide qué tipo de reconocedores mínimos servirían para determinar las cadenas válidas.

Tipo	Nombre	Forma de las producciones	Tipo de autómata o reconocedor
0	LRE	Irrestrictas	Máquina de Turing
1	LDC		Autómata linealmente acotado
2	LLC		Autómata de pila
3	LR	ó	Autómata finito Expresión regular

Hechos que se sostienen en la formalización de Alan Turing con sus autómatas que emulaban diversos procesos algoritmizables, modelos ya demostrados y aceptados en la naciente comunidad de especialistas en computadoras y matemáticas aplicadas a los ordenadores. Este aporte derivado de la visión estructuralista y matemática del momento de realización de esta teoría lingüística encontró su mayor sistema de aplicación en las ciencias de la computación y el desarrollo de las teorías y técnicas de desarrollo de lenguajes de programación y especificado y los compiladores e intérpretes que los procesen, dotándolos de un cuerpo teórico y abriendo las puertas a la gran diversidad de lenguajes de computadora que existen en la actualidad.

Fuentes.

Tanembaum, A. Compilers: Principles, Tecniques, and Tools. Tomo 1. ACM Press. 5ta Edición.
Conferencias de la Asignatura "Compilación 1" del Departamento de Ciencias de la Computación de la Universidad de Oriente. Santiago de Cuba, 2000.
Jerarquía de Chomsky en Wikipedia. Consultado el 20 de febrero de 2012.

This article is issued from Ecured. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.