Matriz identidad

Matriz identidad

Concepto:	Matriz cuadrada cuya diagonal principal contiene solo 1s mientras el resto de las casillas es 0.

Matriz identidad. Dícese de la Matriz cuadrada de orden N cuya diagonal principal contiene únicamente 1s y el resto de la matriz está compuesto exclusivamente por ceros.

Definiciones.

Dada la matriz cuadrada A de orden N se dice que es matriz identidad siempre que todos sus elementos A_i,j cumplan:

A_i,i=1 (celdas de la diagonal principal).
A_i,j=0 para i≠j.

La matriz cuadrada A de orden N se denota I_N .

Ejemplos.

Éstas son I₂, I₃, I₅, respectivamente:

1	0
0	1

1	0	0
0	1	0
0	0	1

1	0	0	0	0
0	1	0	0	0
0	0	1	0	0
0	0	0	1	0
0	0	0	0	1

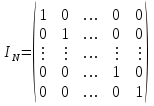
En general I_N tiene la forma:

1	0	...	0	0
0	1	...	0	0
…	…	...	…	…
0	0	...	1	0
0	0	...	0	1

donde pueden apreciarse los 1s característicos en la diagonal principal y los 0s en el resto de la matriz.

Véase también

Fuentes

K. Ribnikov. Análisis Combinatorio. Editorial Mir Moscú. 1988.

This article is issued from Ecured. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.