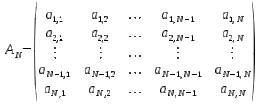Matriz singular
| ||||||
Matriz singular. Es la matriz cuadrada de orden N cuyo determinante es nulo.
En este caso, el sistema de ecuaciones lineales asociado a dicha matriz no tiene solución o tiene infinas soluciones coincidentes.
Definiciones
Dada la matriz cuadrada A de orden N se dice que es matriz singular cuando su determinante es cero.
Ejemplos
En la matriz A:
| 1 | 2 | 3 |
| 4 | 5 | 6 |
| 7 | 8 | 9 |
al calcular su determinante:
- |A| = 1(5x9-8x6)-4(2x9-8x3)+7(2x6-5x3) = 1(45-48)-4(18-24)+7(12-15) = -3-4(-6)+7(-3) = -3+24-21 = 0,
se puede afirmar que A es una matriz singular.
En cambio la matriz M:
| 1 | 2 | 3 |
| 3 | 4 | 5 |
| 5 | 6 | 8 |
tiene |M|=-2, por lo que es no singular.
Véase también
Fuentes
- Colectivo de Autores. Álgebra lineal. Editorial Félix Valera. 2003.
- K. Ribnikov. Análisis Combinatorio. Editorial Mir Moscú. 1988.
This article is issued from
Ecured.
The text is licensed under Creative
Commons - Attribution - Sharealike.
Additional terms may apply for the media files.