Conway circle theorem

In plane geometry, the Conway circle theorem states that when the sides meeting at each vertex of a triangle are extended by the length of the opposite side, the six endpoints of the three resulting line segments lie on a circle whose centre is the incentre of the triangle. The circle on which these six points lie is called the Conway circle of the triangle.[1][2][3] The theorem and circle are named after mathematician John Horton Conway.

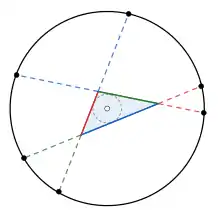
A geometrical diagram showing a circle inside a triangle inside a larger circle.
A triangle's Conway circle with its six concentric points (solid black), the triangle's incircle (dashed gray), and the centre of both circles (white); solid and dashed line segments of the same colour are equal in length

See also

References
  1. "John Horton Conway". www.cardcolm.org. Archived from the original on 20 May 2020. Retrieved 29 May 2020.
  2. Weisstein, Eric W. "Conway Circle". MathWorld. Retrieved 29 May 2020.
  3. Francisco Javier García Capitán (2013). "A Generalization of the Conway Circle" (PDF). Forum Geometricorum. 13: 191–195.


This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.