Matter wave

At the end of the 19th century, light was thought to consist of waves of electromagnetic fields which propagated according to Maxwell's equations, while matter was thought to consist of localized particles (see history of wave and particle duality). In 1900, this division was questioned when, investigating the theory of black-body radiation, Max Planck proposed that the thermal energy of oscillating atoms is divided into discrete portions, or quanta.[4] Extending Planck's investigation in several ways, including its connection with the photoelectric effect, Albert Einstein proposed in 1905 that light is also propagated and absorbed in quanta, now called photons. These quanta would have an energy given by the Planck–Einstein relation:

and a momentum

where ν (lowercase Greek letter nu) and λ (lowercase Greek letter lambda) denote the frequency and wavelength of the light, c the speed of light, and h the Planck constant.[5] In the modern convention, frequency is symbolized by f as is done in the rest of this article. Einstein's postulate was confirmed experimentally by Robert Millikan and Arthur Compton over the next two decades.

Propagation of de Broglie waves in one dimension – real part of the complex amplitude is blue, imaginary part is green. The probability (shown as the color opacity) of finding the particle at a given point x is spread out like a waveform; there is no definite position of the particle. As the amplitude increases above zero the slope decreases, so the amplitude diminishes again, and vice versa. The result is an alternating amplitude: a wave. Top: plane wave. Bottom: wave packet.

De Broglie, in his 1924 PhD thesis,[6] proposed that just as light has both wave-like and particle-like properties, electrons also have wave-like properties. He took the result from special relativity that a body of rest mass m₀ contains an energy E = m₀c² in its rest frame and combined this with the idea that the energy of a quantum is proportional to its frequency. So, he posited, each body rest mass m₀ is associated with some kind of periodic oscillation whose frequency ν₀ is set by hν₀ = m₀c² in the rest frame.[7][8] Thus, it was a simple step to get to the equation that bears his name.[9] Also, by rearranging the momentum equation stated in the above section, we find a relationship between the wavelength, λ, associated with an electron and its momentum, p, through the Planck constant, h:[10]

${\displaystyle \lambda ={\frac {h}{p}}.}$

The relationship has since been shown to hold for all types of matter: all matter exhibits properties of both particles and waves.

When I conceived the first basic ideas of wave mechanics in 1923–1924, I was guided by the aim to perform a real physical synthesis, valid for all particles, of the coexistence of the wave and of the corpuscular aspects that Einstein had introduced for photons in his theory of light quanta in 1905.

— de Broglie[11]

Following up on de Broglie's ideas, physicist Peter Debye made an offhand comment that if particles behaved as waves, they should satisfy some sort of wave equation. Inspired by Debye's remark, Erwin Schrödinger decided to find a proper three-dimensional wave equation for the electron. He was guided by William Rowan Hamilton's analogy between mechanics and optics (see Hamilton–Jacobi equation), encoded in the observation that the zero-wavelength limit of optics resembles a mechanical system – the trajectories of light rays become sharp tracks that obey Fermat's principle, an analog of the principle of least action.[12] In 1926, Schrödinger published the wave equation that now bears his name[13] – the matter wave analogue of Maxwell's equations – and used it to derive the energy spectrum of hydrogen. Frequencies of solutions of the non-relativistic Schrödinger equation differ from de Broglie waves by the Compton frequency since the energy corresponding to the rest mass of a particle is not part of the non-relativistic Schrödinger equation. The Schrödinger equation describes the time evolution of a wavefunction, a function that assigns a complex number to each point in space. Schrödinger tried to interpret the modulus squared of the wavefunction as a charge density. This approach was, however, unsuccessful.[14][15][16] Max Born proposed that the modulus squared of the wavefunction is instead a probability density, a successful proposal now known as the Born rule.[14]

Matter waves were first experimentally confirmed to occur in George Paget Thomson and Alexander Reid's diffraction experiment[1] and the Davisson–Germer experiment,[2][3] both for electrons. The de Broglie hypothesis and the existence of matter waves has been confirmed for other elementary particles, neutral atoms and even molecules have been shown to be wave-like.

Matter wave double slit diffraction pattern building up electron by electron. Each black dot represents a single electron hitting a detector; with a statistically large number of electrons interference fringes appear.[17]

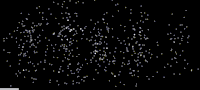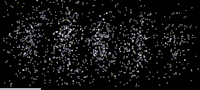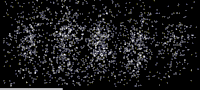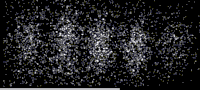
As shown in this image, an especially clear confirmation experiment by Bach et al[17] implemented the famous double-slit experiment[18] using electrons through physical apertures and recorded each particle building up the full diffraction pattern.

In 1927 at Bell Labs, Clinton Davisson and Lester Germer fired slow-moving electrons at a crystalline nickel target.[2][3] The angular dependence of the diffracted electron intensity was measured, and was determined to have a similar angular dependence to diffraction patterns predicted by Bragg for x-rays. At the same time George Paget Thomson and Alexander Reid at the University of Aberdeen were independently firing electrons at thin celluloid foils and later metal films, observing rings which can be similarly interpreted.[1] (Alexander Reid, who was Thomson's graduate student, performed the first experiments but he died soon after in a motorcycle accident[19] and is rarely mentioned.) Before the acceptance of the de Broglie hypothesis, diffraction was a property that was thought to be exhibited only by waves. Therefore, the presence of any diffraction effects by matter demonstrated the wave-like nature of matter. When the de Broglie wavelength was inserted into the Bragg condition, a similar angular dependence to the experimentally observed diffraction pattern was found, thereby experimentally supporting the de Broglie hypothesis for electrons.[20] This was placed onto a solid foundation in 1928 by Hans Bethe,[21] who solved the Schrödinger equation,[13] showing how this could explain the experimental results. His approach is similar to what is used in modern electron diffraction approaches.[22][23]

This was a pivotal result in the development of quantum mechanics. Just as the photoelectric effect demonstrated the particle nature of light, the Davisson–Germer experiment showed the wave-nature of matter, and completed the theory of wave–particle duality. This idea was important because it meant that not only could any particle exhibit wave characteristics, but that one could use wave equations to describe phenomena in matter.

Neutrons, produced in nuclear reactors with around 1MeV energy, thermalize to around 0.025eV as they scatter from light atoms. The resulting de Broglie wavelength (around 180 pm) matches interatomic spacing. In 1944, Ernest O. Wollan, with a background in X-ray scattering from his PhD work[24] under Arthur Compton, recognized the potential for applying thermal neutrons from the newly operational X-10 nuclear reactor to crystallography. Joined by Clifford G. Shull they developed[25] neutron diffraction through out the 1940s.

Experiments with Fresnel diffraction[26] and an atomic mirror for specular reflection[27][28] of neutral atoms confirm the application of the de Broglie hypothesis to atoms, i.e. the existence of atomic waves which undergo diffraction, interference and allow quantum reflection by the tails of the attractive potential.[29] Advances in laser cooling have allowed cooling of neutral atoms down to nanokelvin temperatures. At these temperatures, the thermal de Broglie wavelengths come into the micrometre range. Using Bragg diffraction of atoms and a Ramsey interferometry technique, the de Broglie wavelength of cold sodium atoms was explicitly measured and found to be consistent with the temperature measured by a different method.[30]

This effect has been used to demonstrate atomic holography, and it may allow the construction of an atom probe imaging system with nanometer resolution.[31][32] The description of these phenomena is based on the wave properties of neutral atoms, confirming the de Broglie hypothesis.

The effect has also been used to explain the spatial version of the quantum Zeno effect, in which an otherwise unstable object may be stabilised by rapidly repeated observations.[28]

Recent experiments even confirm the relations for molecules and even macromolecules that otherwise might be supposed too large to undergo quantum mechanical effects. In 1999, a research team in Vienna demonstrated diffraction for molecules as large as fullerenes.[33] The researchers calculated a de Broglie wavelength of the most probable C₆₀ velocity as 2.5 pm. More recent experiments prove the quantum nature of molecules made of 810 atoms and with a mass of 10123 Da.[34] As of 2019, this has been pushed to molecules of 25000 Da.[35]

Using two formulas from special relativity, one for the relativistic mass energy and one for the relativistic momentum

${\displaystyle E=mc^{2}=\gamma m_{0}c^{2}}$

${\displaystyle \mathbf {p} =m\mathbf {v} =\gamma m_{0}\mathbf {v} }$

allows the equations to be written as

${\displaystyle {\begin{aligned}&\lambda =\,\,{\frac {h}{\gamma m_{0}v}}\,=\,{\frac {h}{m_{0}v}}\,\,\,\,{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}\\&f={\frac {\gamma \,m_{0}c^{2}}{h}}={\frac {m_{0}c^{2}}{h{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}}\end{aligned}}}$

where ${\displaystyle m_{0}}$ denotes the particle's rest mass, ${\displaystyle v}$ its velocity, ${\displaystyle \gamma }$ the Lorentz factor, and ${\displaystyle c}$ the speed of light in vacuum.[38][39][40] See below for details of the derivation of the de Broglie relations. Group velocity (equal to the particle's speed) should not be confused with phase velocity (equal to the product of the particle's frequency and its wavelength). In the case of a non-dispersive medium, they happen to be equal, but otherwise they are not.

Albert Einstein first explained the wave–particle duality of light in 1905. Louis de Broglie hypothesized that any particle should also exhibit such a duality. The velocity of a particle, he concluded, should always equal the group velocity of the corresponding wave.

Both in relativistic and non-relativistic quantum physics, we can identify the group velocity of a particle's wave function with the particle velocity. Quantum mechanics has very accurately demonstrated this hypothesis, and the relation has been shown explicitly for particles as large as molecules.[33]

De Broglie deduced that if the duality equations already known for light were the same for any particle, then his hypothesis would hold. This means that

where E is the total energy of the particle, p is its momentum, ħ is the reduced Planck constant. For a free non-relativistic particle it follows that

where m is the mass of the particle and v its velocity.

Also in special relativity we find that

where m₀ is the rest mass of the particle and c is the speed of light in vacuum. But (see below), using that the phase velocity is v_p = E/p = c²/v, therefore

where v is the velocity of the particle regardless of wave behavior.

In quantum mechanics, particles also behave as waves with complex amplitudes. The phase velocity is equal to the product of the frequency multiplied by the wavelength.

By the de Broglie hypothesis, we see that

${\displaystyle v_{\mathrm {p} }={\frac {\omega }{k}}={\frac {E/\hbar }{p/\hbar }}={\frac {E}{p}}.}$

Using relativistic relations for energy and momentum, we have

${\displaystyle v_{\mathrm {p} }={\frac {E}{p}}={\frac {mc^{2}}{mv}}={\frac {\gamma m_{0}c^{2}}{\gamma m_{0}v}}={\frac {c^{2}}{v}}={\frac {c}{\beta }},}$

where E is the total energy of the particle, p the momentum, ${\displaystyle \gamma }$ the Lorentz factor, c the speed of light, and β the speed as a fraction of c. The variable v can either be taken to be the speed of the particle or the group velocity of the corresponding matter wave. Since the particle speed ${\displaystyle v<c}$ for any particle that has nonzero mass (according to special relativity), the phase velocity of matter waves always exceeds c, i.e.,

${\displaystyle v_{\mathrm {p} }>c,}$

which approaches c when the particle speed is relativistic. The superluminal phase velocity does not violate special relativity. See the article on Dispersion (optics) for details.

Using four-vectors, the De Broglie relations form a single equation:

$${\displaystyle \mathbf {P} =\hbar \mathbf {K} ,}$$

which is frame-independent.

Likewise, the relation between group/particle velocity and phase velocity is given in frame-independent form by:

$${\displaystyle \mathbf {K} =\left({\frac {\omega _{0}}{c^{2}}}\right)\mathbf {U} ,}$$

where

• Four-momentum ${\displaystyle \mathbf {P} =\left({\frac {E}{c}},{\vec {\mathbf {p} }}\right)}$
• Four-wavevector ${\displaystyle \mathbf {K} =\left({\frac {\omega }{c}},{\vec {\mathbf {k} }}\right)=\left({\frac {\omega }{c}},{\frac {\omega }{v_{p}}}\mathbf {\hat {n}} \right)}$
• Four-velocity ${\displaystyle \mathbf {U} =\gamma (c,{\vec {\mathbf {u} }})=\gamma (c,v_{g}{\hat {\mathbf {n} }})}$