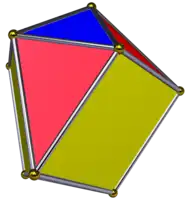
Herschel graph
In graph theory, a branch of mathematics, the Herschel graph is a bipartite undirected graph with 11 vertices and 18 edges. It is a polyhedral graph (the graph of a convex polyhedron), and is the smallest polyhedral graph that does not have a Hamiltonian cycle, a cycle passing through all its vertices. It is named after British astronomer Alexander Stewart Herschel, because of Herschel's studies of Hamiltonian cycles in polyhedral graphs (but not of this graph).
| Herschel graph | |
|---|---|
 The Herschel graph. | |
| Named after | Alexander Stewart Herschel |
| Vertices | 11 |
| Edges | 18 |
| Automorphisms | 12 (D6) |
| Properties | |
| Table of graphs and parameters | |
Definition and properties
The Herschel graph has three vertices of degree four and eight vertices of degree three. Each of the three pairs of degree-four vertices belongs to a cycle of four vertices, alternating with a pair of degree-three vertices. Two degree-three vertices do not participate in these four-vertex cycles; instead, their neighbors are three degree-three vertices, one from each four-vertex cycle.[1]
The Herschel graph is a polyhedral graph; this means that it is a planar graph, one that can be drawn in the plane with none of its edges crossing, and that it is 3-vertex-connected: the removal of any two of its vertices leaves a connected subgraph.[1] It is a bipartite graph: its vertices can be separated into two subsets of five and six vertices respectively, such that every edge has an endpoint in each subset (the red and blue subsets in the picture).[2]
It has order-6 dihedral symmetry, for a total of 12 members of its automorphism group. The degree-four vertices can be permuted arbitrarily, giving six permutations, and in addition, for each permutation of the degree-four vertices, there is a symmetry that keeps these vertices fixed and exchanges pairs of degree-three vertices.[1]
Polyhedron
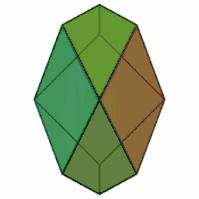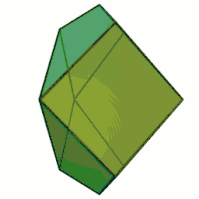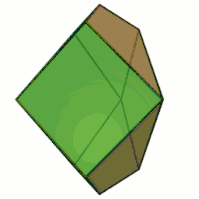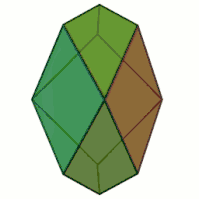
The Herschel graph is planar and 3-vertex-connected, so it follows by Steinitz's theorem that it is a polyhedral graph: there exists a convex polyhedron (an enneahedron) having the Herschel graph as its skeleton.[3] This polyhedron has nine quadrilaterals for faces. If these are chosen so that the polyhedron has all of the same symmetries as the underlying graph, three of the faces will be rhombi or squares, and the other six will be kites.[1]
The dual polyhedron is a rectified triangular prism, which can be formed as the convex hull of the midpoints of the edges of a triangular prism. When constructed in this way, it has three square faces on the same planes as the square faces of the prism, two equilateral triangle faces on the planes of the triangular ends of the prism, and six more isosceles triangle faces. This polyhedron has the property that its faces cannot be numbered in such a way that consecutive numbers appear on adjacent faces, and such that the first and last numbers are also on adjacent faces. Because polyhedral face numberings of this type are used as "spindown life counters" in the game Magic: The Gathering, Constantinides & Constantinides (2018) name the canonical polyhedron realization of this dual polyhedron as "the Lich's nemesis".[4]
Hamiltonicity

As a bipartite graph that has an odd number of vertices, the Herschel graph does not contain a Hamiltonian cycle (a cycle of edges that passes through each vertex exactly once). For, in any bipartite graph, any cycle must alternate between the vertices on either side of the bipartition, and therefore must contain equal numbers of both types of vertex and must have an even length. Thus, a cycle passing once through each of the eleven vertices cannot exist in the Herschel graph. It is the smallest non-Hamiltonian polyhedral graph, whether the size of the graph is measured in terms of its number of vertices, edges, or faces.[5] There exist other polyhedral graphs with 11 vertices and no Hamiltonian cycles (notably the Goldner–Harary graph)[6] but none with fewer edges.[3]
All but three of the vertices of the Herschel graph have degree three. Tait's conjecture[7] states that a polyhedral graph in which every vertex has degree three must be Hamiltonian, but this was disproved when W. T. Tutte provided a counterexample, the much larger Tutte graph.[8] A refinement of Tait's conjecture, Barnette's conjecture that every bipartite 3-regular polyhedral graph is Hamiltonian, remains open.[9]
Every maximal planar graph that does not have a Hamiltonian cycle has a Herschel graph as a minor. The Herschel graph is conjectured to be one of three minor-minimal non-Hamiltonian 3-vertex-connected graphs. The other two are the complete bipartite graph and a graph formed by splitting both the Herschel graph and into two symmetric halves by three-vertex separators and then combining one half from each graph.[10]

The Herschel graph also provides an example of a polyhedral graph for which the medial graph has no Hamiltonian decomposition into two edge-disjoint Hamiltonian cycles. The medial graph of the Herschel graph is a 4-regular graph with 18 vertices, one for each edge of the Herschel graph; two vertices are adjacent in the medial graph whenever the corresponding edges of the Herschel graph are consecutive on one of its faces.[11] It is 4-vertex-connected and essentially 6-edge-connected, meaning that for every partition of the vertices into two subsets of at least two vertices, there are at least six edges crossing the partition.[12]
History
The Herschel graph is named after British astronomer Alexander Stewart Herschel, who wrote an early paper concerning William Rowan Hamilton's icosian game. This is a puzzle involving finding Hamiltonian cycles on a polyhedron, usually the regular dodecahedron. The Herschel graph describes the smallest convex polyhedron that can be used in place of the dodecahedron to give a game that has no solution. However, Herschel's paper described solutions for the Icosian game only on the graphs of the regular tetrahedron and regular icosahedron; it did not describe the Herschel graph.[13] The name "the Herschel graph" makes an early appearance in a graph theory textbook by John Adrian Bondy and U. S. R. Murty, published in 1976.[14] However, the graph itself was described earlier, for instance by H. S. M. Coxeter.[3]
References
- Lawson-Perfect, Christian (13 October 2013), "An enneahedron for Herschel", The Aperiodical, retrieved 7 December 2016
- Holton, D. A. (1983), "Cycles in graphs", in Casse, L. R. A. (ed.), Combinatorial Mathematics X: Proceedings of the Conference Held in Adelaide, Australia, August 23-27, 1982, Lecture Notes in Mathematics, vol. 1036, Berlin: Springer, pp. 24–48, doi:10.1007/BFb0071507, MR 0731570
- Coxeter, H. S. M. (1973), Regular Polytopes, Dover, p. 8
- Constantinides, Anthony F.; Constantinides, George A. (October 2018), "Spindown Polyhedra", The Mathematical Gazette, 102 (555): 447–453, doi:10.1017/mag.2018.111, S2CID 233357977
- Barnette, David; Jucovič, Ernest (1970), "Hamiltonian circuits on 3-polytopes", Journal of Combinatorial Theory, 9 (1): 54–59, doi:10.1016/S0021-9800(70)80054-0.
- Goldner, A.; Harary, F. (1975), "Note on a smallest nonhamiltonian maximal planar graph", Bull. Malaysian Math. Soc., 6 (1): 41–42; see also the same journal 6(2):33 (1975) and 8:104-106 (1977). Reference from listing of Harary's publications.
- Tait, P. G. (1884), "Listing's Topologie", Philosophical Magazine, 5th Series, 17: 30–46; reprinted in Scientific Papers, vol. II, pp. 85–98
- Tutte, W. T. (1946), "On Hamiltonian circuits", Journal of the London Mathematical Society, 21 (2): 98–101, doi:10.1112/jlms/s1-21.2.98
- Samal, Robert (11 June 2007), Barnette's conjecture, the Open Problem Garden, retrieved 24 Feb 2011
- Ding, Guoli; Marshall, Emily (2018), "Minimal -connected non-Hamiltonian graphs", Graphs and Combinatorics, 34 (2): 289–312, doi:10.1007/s00373-018-1874-z, MR 3774453, S2CID 253891751
- Bondy, J. A.; Häggkvist, R. (1981), "Edge-disjoint Hamilton cycles in 4-regular planar graphs", Aequationes Mathematicae, 22 (1): 42–45, doi:10.1007/BF02190157, S2CID 120729891.
- Király, Csaba; Péterfalvi, Ferenc (2012), "Balanced generic circuits without long paths", Discrete Mathematics, 312 (15): 2262–2271, doi:10.1016/j.disc.2012.03.031, MR 2926099
- Herschel, A. S. (1862), "Sir Wm. Hamilton's Icosian Game", The Quarterly Journal of Pure and Applied Mathematics, 5: 305
- Bondy, J. A.; Murty, U. S. R. (1976), Graph Theory With Applications, North Holland, p. 53, MR 0411988