Torsion constant
The torsion constant or torsion coefficient is a geometrical property of a bar's cross-section. It is involved in the relationship between angle of twist and applied torque along the axis of the bar, for a homogeneous linear elastic bar. The torsion constant, together with material properties and length, describes a bar's torsional stiffness. The SI unit for torsion constant is m4.
History
In 1820, the French engineer A. Duleau derived analytically that the torsion constant of a beam is identical to the second moment of area normal to the section Jzz, which has an exact analytic equation, by assuming that a plane section before twisting remains planar after twisting, and a diameter remains a straight line. Unfortunately, that assumption is correct only in beams with circular cross-sections, and is incorrect for any other shape where warping takes place.[1]
For non-circular cross-sections, there are no exact analytical equations for finding the torsion constant. However, approximate solutions have been found for many shapes. Non-circular cross-sections always have warping deformations that require numerical methods to allow for the exact calculation of the torsion constant.[2]
The torsional stiffness of beams with non-circular cross sections is significantly increased if the warping of the end sections is restrained by, for example, stiff end blocks.[3]
Formulation
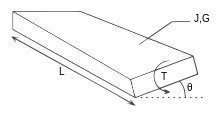
For a beam of uniform cross-section along its length, the angle of twist (in radians) is:
where:
- T is the applied torque
- L is the beam length
- G is the modulus of rigidity (shear modulus) of the material
- J is the torsional constant
Inverting the previous relation, we can define two quantities; the torsional rigidity,
- with SI units N⋅m2/rad
And the torsional stiffness,
- with SI units N⋅m/rad
Examples
Bars with given uniform cross-sectional shapes are special cases.
Circle
where
- r is the radius
This is identical to the second moment of area Jzz and is exact.
alternatively write: [4] where
- D is the Diameter
Rectangle
where
- a is the length of the long side
- b is the length of the short side
- is found from the following table:
| a/b | |
|---|---|
| 1.0 | 0.141 |
| 1.5 | 0.196 |
| 2.0 | 0.229 |
| 2.5 | 0.249 |
| 3.0 | 0.263 |
| 4.0 | 0.281 |
| 5.0 | 0.291 |
| 6.0 | 0.299 |
| 10.0 | 0.312 |
| 0.333 |
Alternatively the following equation can be used with an error of not greater than 4%:
where
- a is the length of the long side
- b is the length of the short side
Thin walled open tube of uniform thickness
- [8]
- t is the wall thickness
- U is the length of the median boundary (perimeter of median cross section)
Circular thin walled open tube of uniform thickness
This is a tube with a slit cut longitudinally through its wall. Using the formula above:
- [9]
- t is the wall thickness
- r is the mean radius
References
- Archie Higdon et al. "Mechanics of Materials, 4th edition".
- Advanced structural mechanics, 2nd Edition, David Johnson
- The Influence and Modelling of Warping Restraint on Beams
- "Area Moment of Inertia." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/AreaMomentofInertia.html
- Roark's Formulas for stress & Strain, 7th Edition, Warren C. Young & Richard G. Budynas
- Continuum Mechanics, Fridtjov Irjens, Springer 2008, p238, ISBN 978-3-540-74297-5
- Advanced Strength and Applied Elasticity, Ugural & Fenster, Elsevier, ISBN 0-444-00160-3
- Advanced Mechanics of Materials, Boresi, John Wiley & Sons, ISBN 0-471-55157-0
- Roark's Formulas for stress & Strain, 6th Edition, Warren C. Young