Autómata finito determinista

Autómata finito determinista

Concepto:	Reconocedor de lenguajes regulares que no usa memoria para almacenar los estados de ejecución ni los símbolos del lenguaje y cuyas transiciones son unívocas y no vacías.

Autómata finito determinista. Es el autómata finito que tiene todas sus transiciones no vacías y que por cada símbolo desde un estado de origen se llega a un único estado destino.

Los AFD son definiciones ideales dentro de los lenguajes regulares por su cercanía formal hacia la creación de máquinas de reconocimiento fundamentalmente lexicográficas, en tanto sus transiciones son únicas por símbolo, pudiendo a la hora de su implementación en software, matemática y física realizarse con mayor facilidad.

Definición

Sea un autómata finito definido por la 5-tupla A=<Q, T, g, F, q₀>, donde Q es el conjunto de estados, T el alfabeto de símbolos terminales, la relación de transiciones ó (léase: del estado q_i mediante el terminal x se va a q_j), F son los estados finales o de llegada dentro de Q, q₀ es el estado inicial o de partida; se dice que A es un autómata finito determinista (AFD) si y sólo si se satisface en g las siguientes propiedades:

Toda transición de g no es vacía (cosa que se cumple en este caso, debido a la definición particular de g que excluye de los símbolos de transición a las cadenas vacías, cosa que no sucede en la definición general de autómata finito donde ).
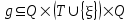
Desde cualquier estado y con el mismo terminal solo se va a uno y solo un estado, es decir .

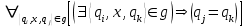
En términos planos, esto significa que solo se podrá ir desde un estado A mediante el terminal x a un único estado B:

y los siguientes casos:

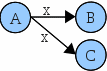
<A,, B>.

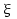
son transiciones de autómatas finitos no deterministas.

Consecuencias

La definición formal de AFD se basa en la consideración de que las transiciones múltilples para un mismo símbolo y las vacías son indeseables sobre todo para la implementación material, fundamentalmente mecánica, de los autómatas finitos. En caso de uno de los usos más frecuentes de éstos, la modelación de analizadores lexicográficos de los elementos gramaticales de los lenguajes de programación, la exclusión del indeterminismo libra al sistema de dicho comportamiento y lo hace más específico y por tanto más potente.

Una resultante evidente de la definición AFD es que en las tablas de transición de los mismos no hay más que un estado en cada casilla, haciendo más clara la interpretación y reconocimiento de cadenas mediante el reconocedor.

En definitiva, los AFD son los autómatas finitos ideales, aunque no siempre pueden formalizarse a la primera y en no pocas ocasiones son el resultado de la depuración de AFND y de AFNDTV. Donde es bueno señalar que esta transformación siempre es posible.

Transformación de AFD a gramáticas regulares.

Sea un AFD A=<Q, T, g, F, q₀>, éste puede transformarse a gramática regular G=<Q, T, P,q₀> (Q, conjunto de no terminales; T, conjunto de símbolos terminales; P, sistema de producciones de G y q₀ es el símbolo de inicio), como puede verse los elementos de la 5-tupla del autómata finito se transforman directamente a los de la 4-upla de la grámatica regular. Luego el sistema de producciones P se contruye a partir de las transiciones g mediante los pasos:

Transición: <A,x,B> ó se convierte en .
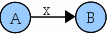
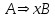
Transición a estado final: <A,x,B> donde B es un estado final, ó se convierte en .
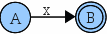
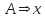
Lazo: <A,x,A> ó se convierte en .
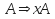
Lazo en estado final: <A,x,A> donde A es un estado final, ó se convierte en .

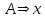
Véase también

Lenguaje regular.
Gramática regular.
Expresión regular.
Diagrama de estados.
Autómata finito.
Autómata finito no determinista.
Autómata finito no determinista con transición vacía (AFND-TV ó ).

Fuentes

Tanembaum, A. Compilers: Principles, Techniques, and Tools. Tomo 1. ACM Press. 5ta Edición.
Conferencias de la Asignatura "Compilación 1" del Departamento de Ciencias de la Computación de la Universidad de Oriente. Santiago de Cuba, 2000.
Autómata finito en Wikipedia. Consultado el 25 de noviembre de 2013.
Acevedo Martínez, Liesner; Osorio Ramírez, Karel. Manual de apoyo a la docencia. Técnicas de Compilación: Manual Práctico para estudiantes de Informática. Libro electrónico en PDF. UCI. La Habana, 2011.

This article is issued from Ecured. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.