Autómata finito no determinista

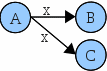
Autómata finito no determinista

Concepto:	Reconocedor de lenguajes regulares que no usa memoria para almacenar los estados de ejecución ni los símbolos del lenguaje, con transiciones no unívocas o vacías.

Autómata finito no determinista. Es el autómata finito que tiene transiciones vacías o que por cada símbolo desde un estado de origen se llega a más de un estado destino.

Los AFND son definiciones no tan deseables dentro de los lenguajes regulares porque dificultan su implementación tanto mecánica como informática; aunque en la mayoría de las transformaciones a lo interno de los LR (expresiones regulares a AF, gramáticas regulares a AF) conducen a AFND. Los AFND, por tanto, son imprescindibles en el análisis lexicográfico y el diseño de los lenguajes de programación.

Definición

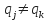
Sea un autómata finito definido por la 5-tupla A=<Q, T, g, F, q₀>, donde Q es el conjunto de estados, T el alfabeto de símbolos terminales, la relación de transiciones ó (léase: del estado q_i mediante el terminal x se va a q_j), F son los estados finales o de llegada dentro de Q, q₀ es el estado inicial o de partida; se dice que A es un autómata finito no determinista (AFND) si y sólo si existen en g al menos una de las siguientes transiciones:

ó <q_i,x,q_j> y <q_i,x,q_k> son transiciones de g y .
<q_i,,q_j>.

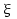
Consecuencias

La definición formal de AFND se basa en la consideración de que a menudo según los algoritmos de transformación de expresiones y gramáticas regulares a AF terminan obteniéndose autómatas con transiciones múltiples para un mismo símbolo o transiciones vacías. Independientemente que sean indeseables, sobre todo para la implementación material, fundamentalmente mecánica, de los autómatas finitos, son imprescindibles durante la modelación de analizadores lexicográficos de los elementos gramaticales de los lenguajes de programación, llamados tókenes, como literales numéricos, identificadores, cadenas de texto, operadores, etc.

Vease también

Lenguaje regular.
Gramática regular.
Expresión regular.
Diagrama de estado.
Autómata finito.
Autómata finito determinista.
Autómata finito no determinista con transición vacía (AFND-TV ó ).

Fuentes

Tanembaum, A. Compilers: Principles, Tecniques, and Tools. Tomo 1. ACM Press. 5ta Edición.
Conferencias de la Asignatura "Compilación 1" del Departamento de Ciencias de la Computación de la Universidad de Oriente. Santiago de Cuba, 2000.
Autómata finito en Wikipedia.
Acevedo Martínez, Liesner; Osorio Ramírez, Karel. Manual de apoyo a la docencia. Técnicas de Compilación: Manual Práctico para estudiantes de Informática. Libro electrónico en PDF. UCI. La Habana, 2011.

This article is issued from Ecured. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.