Integrales de funciones trigonométricas
| ||||||
Integración de funciones trigonométricas. Una integral se denomina trigonométrica cuando el integrando de la misma está compuesto de funciones trigonométricas y constantes..
Definición
Una integral se denomina trigonométrica cuando el integrando de la misma está compuesto de funciones trigonométricas y constantes. Para su resolución desde luego que son válidos los teoremas de integración.
En lo general se deben aplicar las siguientes sugerencias:
1. Usar una identidad trigonométrica y simplificar, es útil cuando se presentan funciones trigonométricas.
2. Eliminar una raíz cuadrada, se presenta normalmente después de completar un cuadrado o una sustitución trigonométrica.
3. Reducir una fracción impropia.
4. Separar los elementos del numerador de una fracción entre el denominador de la fracción.
5. Multiplicar por una forma unitaria g(x)/g(x) que al multiplicar por el integrando f(x) permita modificar adecuadamente [f(x)g(x)]/g(x).
6. Probar sustituir f(x) por 1/(1/f(x)).
Es necesario tener siempre a la mano una tabla de identidades trigonométricas y sustituyendo adecuadamente, llegarás a las “fórmulas básicas”.
Potencias pares de sen x o cos x
Se aplica el seno y coseno del ángulo mitad:
![]()
Ejemplo
1. Encuentre:
![]()
Solución:


Potencias impares de sen x o cos x
Se relacionan el seno y coseno mediante la fórmula:
![]()
Ejemplo
1. Encuentre:
![]()
Solución:
![]()
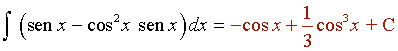
Con exponente par e impar
El exponente impar se transforma en uno par y otro impar.
Ejemplo
1. Encuentre:
![]()
Solución:
![]()
![]()
![]()

Productos de tipo sen(nx) · cos(mx)
Se transforman los productos en sumas:
![]()
![]()
![]()
Ejemplo
1. Encuentre:
![]()
Solución:

Vea también
- Integración de funciones racionales
