Logaritmo complejo
| ||||||
Logaritmo complejo. En Matemáticas y más específicamente Análisis Matemático es la versión del logaritmo sobre el conjunto de los números complejos.
El mismo tiene sus bases en la representación exponencial de los números complejos y su relación con la forma trigonométrica (Ley de Euler), junto con las propiedades ya conocidas en los números reales de los logaritmos.
Resulta de vital importancia para la extensión de las operaciones de logaritmación de argumentos reales positivos y negativos y también en la formulación de otras funciones complejas las trigonométricas inversas complejas y otras.
Definición
A la relación funcional ![]()
- Si logba=c entonces bc=a, donde a,b y c son todos complejos y b no es 0 ni a tampoco.
se le denomina logaritmo complejo de a en base b.
Cuando b=e entonces se le llama logaritmo neperiano complejo y se denota simplemente ln a.
Para este último caso, tenemos que para todo complejo no nulo ![]()

Dadas las propiedades de los logaritmos se puede aprovechar el resultado anterior para definir el algoritmo complejo general en función del neperiano:
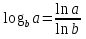
Importancia
Los logaritmos complejos expanden los resultados de la función logaritmo real a resultados no previstos antes como lo puede ser los logaritmos negativos. También su definición sirve para declarar las funciones trigonométricas inversas complejas.
Logaritmos de reales negativos
Para determinar el logaritmo de un real negativo -x se comienza por expresar el producto como (-1)x y luego su representación compleja como x(-1+0i)=x(cos b +isen b), donde x>0. Luego, el primer ángulo b que produce cos b =-1 y sen b=0 es 1800 o en radianes, ![]()
Escribiendo todo en notación exponencial queda:
Entonces el logaritmo de -x se calcula mediante la expresión (*) como:
Funciones trigonométricas inversas complejas
Las funciones trigonométricas inversas sobre los complejas se calculan mediante logaritmos complejos como se ve en las expresiones:
De forma similar se declaran las funciones trigonométricas hiperbólicas inversas:
Veáse también
Fuentes
- I. Bronshtein, K. Semendiaev. Manual de matemáticas para ingenieros y estudiantes. 2da Edición. Editorial MIR, Moscú. 1973.
- . Disponible en "es.wikipedia.org". Consultado 1 de diciembre de 2014.
- . Disponible en "es.wikipedia.org". Consultado 1 de diciembre de 2014.
- . Disponible en "es.wikipedia.org". Consultado 1 de diciembre de 2014.
- . Disponible en "es.wikipedia.org". Consultado 1 de diciembre de 2014.
