Métrica binaria
| ||||||
Métrica binaria. En Matemáticas, Álgebra, Geometría y más específicamente, Topología se trata de una magnitud y su ley que determina el menor nivel de diferencia o lejanía entre dos objetos de un espacio o geometría dados, usualmente considerados como puntos, en este caso mediante el resultado de la igualdad o desigualdad pura de ambos.
Es la más elemental de las métricas, por lo que su campo de utilidad es más teórico que práctico, aunque se usa en el reconocimiento de patrones y la minería de datos de la inteligencia artificial.
Definiciones
Se denomina métrica o distancia binaria a toda función binaria d(x,y), donde x e y son elementos de un conjunto no vacío A, que sea definida de la forma:
O dicho de una manera más simple: la distancia entre dos elementos es 0 si son iguales o de lo contrario, están alejados en 1 unidad.
Importancia
La métrica binaria es la más sencilla en su expresión y significación de todas las manifestaciones de métricas. No obstante su simplicidad y a su aparente poco significado práctico es usado de manera elemental en formulaciones de espacios métricos y en aplicaciones de inteligencia artificial, matemática discreta y lógica.
Como distancia al fin y al cabo satisface las 5 propiedades de la misma:
- No negatividad:
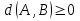
- Simetría: d(x,y)=d(y,x).
- Reflexividad: d(x,x)=0.
- Desigualdad triangular:
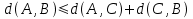
- Implicación de reflexividad: Si d(x,y)=0, entonces x=y.
La demostración de las cinco propiedades inherentes a las métricas aunque evidentes se exponen a continuación.
Prueba de la condición de distancia
La prueba de que la métrica lógica o binaria es una métrica viene dada por los siguientes pasos.
Por la misma definición, puede apreciarse que se satisfacen las propiedades 1, 2, 3 y 5. Ahora en la comprobación de la 4ta propiedad (la desigualdad triangular) se parte de la expresión original:
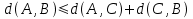
expresión que puede ser evaluada con cualquiera de las siguientes combinaciones de valores:
| d(x,y) | d(x,z) | d(z,y) | |
|---|---|---|---|
| 0 | 0 | 0 | |
| 0 | 1 | 0 | Verdadero en cálculo. Caso imposible, incumple la relación de igualdad que es transitiva |
| 0 | 0 | 1 | Verdadero en cálculo. Caso imposible, incumple la relación de igualdad que es transitiva |
| 0 | 1 | 1 | |
| 1 | 1 | 0 | |
| 1 | 0 | 1 | |
| 1 | 1 | 1 |
Lo que queda demostrado.
Veáse también
- Métrica.
- Métrica euclideana.
- Métrica de Mahalanobis.
- Métrica esférica.
- Espacio métrico.
Fuentes
- I. Bronshtein, K. Semendiaev. Manual de matemáticas para ingenieros y estudiantes. 2da Edición. Editorial MIR, Moscú. 1973.
- Russell S. J.; Norvig, P. Inteligencia artificial, un enfoque moderno. 2da Edición. Pearson Educación SA, Madrid. 2004.
- Distancia en Wikipedia. Revisado 29 de mayo de 2012.
