Subgrupo
| ||||||
Subgrupo. En Álgebra dícese de la estructura algebraica conformada por el par <G',*>, tales que G' es un subconjunto no vacío de G y * es una operación binaria y <G,*> es un grupo y se cumple que <G',*> es también un grupo.
En el caso que <G',*> sea subgrupo y la operación sea conmutativa dentro de G' se está en presencia de un subgrupo conmutativo o abeliano.
Definición.
- Sea un conjunto G y la operación binaria * un grupo algebraico <G,*>, se le llama subgrupo a cualquier

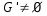
Una consecuencia de importancia en los subgrupos es la siguiente:
- En todo subgrupo <G',*> de <G,*> se cumple

A ese subgrupo se le nombra subgrupo trivial de G para la operación * y se considera la demostración de que todo grupo tiene al menos un subgrupo.
Ejemplos.
Ejemplo 1.
El menor de los subgrupos del grupo <G,*> es <{e},*> donde e es el elemento neutro para * en G, es decir el subgrupo trivial.
Ejemplo 2.
Sea el grupo <{0;1;2;3;4},+5> cuya operación +5 (suma módulo 5) viene definida por la tabla:
| +5 | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 0 | 0 | 1 | 2 | 3 | 4 |
| 1 | 1 | 2 | 3 | 4 | 0 |
| 2 | 2 | 3 | 4 | 0 | 1 |
| 3 | 3 | 4 | 0 | 1 | 2 |
| 4 | 4 | 0 | 1 | 2 | 3 |
no tiene otro subgrupo que el trivial, porque para el resto de los subconjuntos de G se incumple el axioma del cierre de los grupos.
Ejemplo 3.
Sea el grupo <{e,a,b,c},@> (Grupo Cuarto de Klein) con @ definida según la tabla siguiente:
| @ | e | a | b | c |
|---|---|---|---|---|
| e | e | a | b | c |
| a | a | e | c | b |
| b | b | c | e | a |
| c | c | b | a | e |
tiene a <{e},@>, <{e,a},@>, <{e,a,b},@> por subgrupo.
Fuentes
- Subgrupo
- Carl B. Allendoerfer, Cletus O. Oakley. Introducción moderna a la matemática superior. Ediciones del Castillo, Madrid. 1967.
