Teorema fundamental del álgebra

Teorema fundamental del álgebra
Concepto:Todo polinomio no constante de una variable tiene al menos una raíz.
Teorema fundamental del álgebra de los números complejos
Concepto:Todo polinomio de cualesquiera coeficientes numéricos, cuyo grado no sea menor que la unidad, tiene por lo menos una raíz, generalmente, compleja

[1]

Teorema fundamental del Álgebra. En Matemáticas y más especifícamente Álgebra superior, Análisis Matemático, Geometría y funciones de variable compleja, es un teorema que plantea que todo polinomio no constante de una variable tiene al menos una raíz.

Del presente se deriva que todo polinomio p(x) de una variable no constante tiene la misma cantidad de raíces reales o complejas que su grado n, resultado teórico que es vital para el cálculo matemático.



Definiciones

Sea el polinomio de grado n (n>0) de una variable:

  • p(x)=a0+a1x+a2x2+...+anxn.

Existe un número r tal que p(r)=0 o lo que es lo mismo, pero expresado como una factorización:

  • p(x)=(x-r)(b0+b1x+...+bn-1xn-1)

Importancia

De la última definición se desprende que si p(x) puede expresarse como:

  • p(x)=(x-r1)(b0+b1x+...+bn-1xn-1)

resultando un nuevo polinomio p1(x):

  • p1(x)=b0+b1x+...+bn-1xn-1

de grado n-1; entonces a este nuevo polinomio puede aplicarsele el mismo teorema obteniendo una nueva raíz r2 de manera que se podría expresar p(x) de la forma:

  • p(x)=(x-r1)(x-r2)p2(x)

y así descomponiendo sucesivamente los subpolinomios resultantes pi(x) (0<i<n), hasta tener n raíces para p(x) quien podría expresarse a partir del producto de una serie de polimonios lineales tal y como sigue:

  • p(x)=(x-r1)(x-r2)...(x-rn)

Aunque ya se ha mencionado las raíces ri (0<i<n+1) pueden ser reales o complejas y puede darse el caso de que algunas raíces sean iguales como por ejemplo las raíces de los polinomios cuádraticos de la forma trinomio cuadrado perfecto a2x2+2abx+b2 ó a2x2-2abx+b2.

Esta asociación directa entre el grado del polinomio y la cantidad de raíces suyas es de vital importancia tanto para las matemáticas como para otras ramas en las que se modela el comportamiento de algún fenómeno con polinomios.

Otro aspecto es el hecho de la paridad de las raíces complejas que indica que:

  • Si z es una raíz compleja del polinomio p(x), entonces su conjugada también es raíz de p(x).

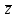
Esto puede apreciarse en el caso en que las ecuaciones de segundo grado ax2+bx+c=0, al calcularsele el discriminante D=b2-4ac<0, entonces solo se satisface con los complejos:

que como se ve son conjugadas.

Veáse también

Referencias

  1. ↑ A. G. Kurosch: Curso de álgebra superior

Fuentes

This article is issued from Ecured. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.