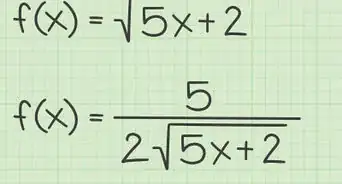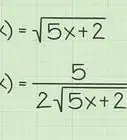How to Find Inflection Points

Co-authored by Hannah Madden

Last Updated: May 6, 2022 References

In calculus, an inflection point is a point on a curve where the slope changes sign.^{[1]
X
Research source} It is used in various disciplines, including engineering, economics, and statistics, to determine fundamental shifts in data. If you remember what concavity is and how it affects inflection, you’ll be able to find the inflection points of the curve with a few simple equations.

Method 1

Method 1 of 5:

Reviewing Concavity and Inflection

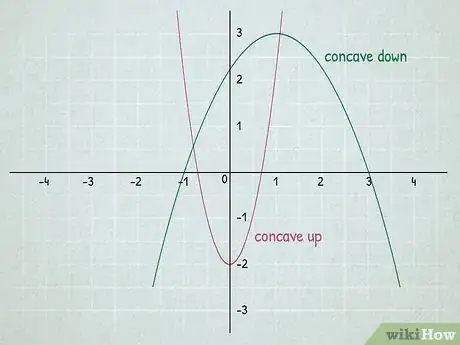
1
Differentiate between concave up and concave down. To understand inflection points, you need to distinguish between these two. They’re easy to distinguish based on their names.^{[2]
X
Research source}
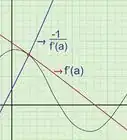
- A concave down function is a function where no line segment that joins 2 points on its graph ever goes above the graph. Intuitively, the graph is shaped like a hill.
- A concave up function, on the other hand, is a function where no line segment that joins 2 points on its graph ever goes below the graph. It is shaped like a U.
- In the graph above, the red curve is concave up, while the green curve is concave down.
- Functions in general have both concave up and concave down intervals. Inflection points exist when a function changes concavity.
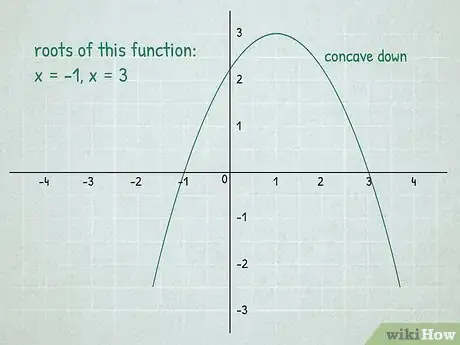
2
Identify the roots of a function. A root of a function is the point where the function equals zero. In the graph above, we can see that the roots of the green parabola are at $x=-1$ $x=-1$ and $x=3.$ $x=3.$ These are the points at which the function intersects the x-axis.^{[3]
X
Research source}
- A function can also have more than 1 root.
Advertisement
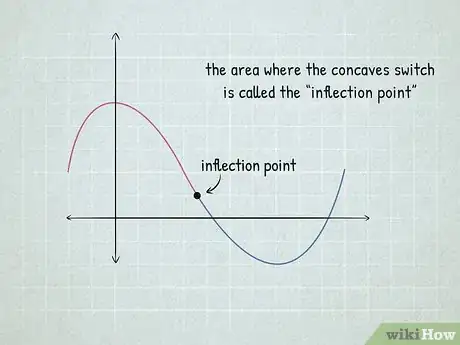
3
Find inflection where the function changes concavity. Remember how there’s a difference between concave up and concave down? The area where the concaves switch is called the “inflection point,” which is what you’re trying to find.^{[4]
X
Research source}
- It’s easy to see this point on a graph.

Method 2

Method 2 of 5:

Finding the Derivatives of a Function

1
Differentiate. Before you can find an inflection point, you’ll need to find derivatives of your function. The derivatives of the basic functions can be found in any calculus text; you’ll need to learn them before you can move on to more complex tasks.^{[5]
X
Research source} First derivatives are denoted as $f^{\prime }(x)$ $f^{{\prime }}(x)$ or ${\frac {\mathrm {d} f}{\mathrm {d} x}}.$ ${\frac {{\mathrm {d}}f}{{\mathrm {d}}x}}.$
- Say you need to find the inflection point of the function below.
  - $f(x)=x^{3}+2x-1$
- Use the power rule.
  - ${\begin{aligned}f^{\prime }(x)&=3x^{3-1}+2x^{1-1}\\&=3x^{2}+2\end{aligned}}$
2
Differentiate again. The second derivative is the derivative of the derivative, and is denoted as $f^{\prime \prime }(x)$ $f^{{\prime \prime }}(x)$ or ${\frac {\mathrm {d} ^{2}f}{\mathrm {d} x^{2}}}.$ ${\frac {{\mathrm {d}}^{{2}}f}{{\mathrm {d}}x^{{2}}}}.$
- ${\begin{aligned}f^{\prime \prime }(x)&=(2)(3)x^{2-1}\\&=6x\end{aligned}}$
3
Set the second derivative equal to 0, and solve the resulting equation. Your answer will be a possible inflection point. ^{[6]
X
Research source}
- ${\begin{aligned}6x&=0\\x&=0\end{aligned}}$

Method 3

Method 3 of 5:

Finding an Inflection Point

1
Check if the second derivative changes sign at the candidate point. If the sign of the second derivative changes as you pass through the candidate inflection point, then there exists an inflection point. If the sign does not change, then there exists no inflection point.^{[7]
X
Research source}
- Remember that you are looking for sign changes, not evaluating the value. In more complicated expressions, substitution may be undesirable, but careful attention to signs often nets the answer much more quickly. For example, instead of evaluating numbers immediately, we could instead look at certain terms and judge them to be positive or negative.
- In our example, $f^{\prime \prime }(x)=6x.$ Then plugging a negative $x$ yields a negative $f^{\prime \prime }(x),$ while plugging a positive $x$ yields a positive $f^{\prime \prime }(x).$ Therefore, $x=0$ is an inflection point of the function $f(x)=x^{3}+2x-1.$ There was no need to actually evaluate for our chosen values.
2
Substitute it back into the original function.^{[8]
X
Research source}
- $f(0)=(0)^{3}+2(0)-1=-1.$
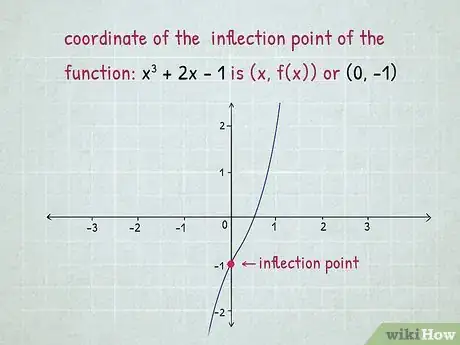
3
Evaluate the function to find the inflection point. The coordinate of the inflection point is denoted as $(x,f(x)).$ In this case, $(0,-1),$ as graphed above. Therefore, those numbers are the inflection point.^{[9]
X
Research source}

Method 4

Method 4 of 5:

Troubleshooting

1
Check the candidates. Often, when $x=0,$ $x=0,$ it is easy to assume that means there are no inflection points. However, when $x=0,$ $x=0,$ there is still an inflection point. Remember, 0 can be graphed, so if you get 0 as your answer, it means there is 1 inflection point.^{[10]
X
Research source}
- For example, if you do get an answer where $x=0,$ you would test the subintervals by graphing $(-infinity,0)$ and $(0,infinity)$ . Therefore, the inflection point is at 0.
2
Include points where the derivative is undefined. When you solve for an inflection point, you have to look for instances when the second derivative is 0 and when the second derivative is undefined. If you only look for ones where the second derivative is 0, chances are, you’ll get the wrong answer.^{[11]
X
Research source}
- For example, if you were given the task of finding whether or not $h(x)=x^{2}+4x$ has an inflection point, you’d consider $h^{\prime \prime }$ , NOT $h^{\prime }$ . This is because $h^{\prime \prime }$ is the second derivative, while $h^{\prime }$ is the relative minimum point (which you aren’t looking for here).
3
Analyze the second derivative, not the first one. When you’re finding inflection points, you should always be considering the second derivative. If you consider the first one, your answer will give you extremum points instead.^{[12]
X
Research source}
- For example, if your possible inflection points are $x=-1$ and $x=7,$ you would test the x values at $(-infinity,-1),(-1,7),$ and $(7,infinity).$ This would tell you that your second derivative has inflection points at both $x=-1$ AND $x=7.$

Method 5

Method 5 of 5:

Using a Scientific Calculator

1
Head to your “Plots.” On most scientific calculators, this will involve hitting the diamond or the second button, then clicking F1. This should take you to your Y plots where you can enter up to 7 values.^{[13]
X
Research source}
- This is true on both the TI-84 and the TI-89, but it may not be the exact same on older models.
2
Enter the function into y1. Clear out any remaining functions you had in your y plots, then type in the function after the equal sign into your calculator. Remember to keep any parentheses involved in the function so your answer is correct.^{[14]
X
Research source}
- For example, the function might be $y1=x^{3}-9/2x^{2}-12x+3$
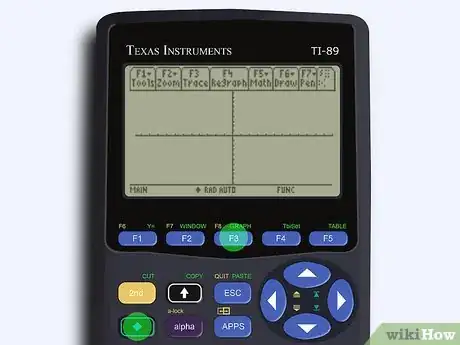
3
Click “graph.” On most calculators, this will be “diamond” or “second,” then F3. If you have to adjust your window on the calculator, press “diamond” or “second,” then F2, then select “standard zoom.”^{[15]
X
Research source}
- Don’t worry if your screen doesn’t show the whole graph just yet—you’ll be able to adjust it.
4
Adjust the window until you can see the whole graph. When you open up the graphing window, you might not be able to see the entire curve of your graph. If that’s the case, click the “diamond” or “second” button, then open up F2 for zoom again. You can increase and decrease your minimum and maximum axis to figure out where your graph will fit inside of the window.^{[16]
X
Research source}
- You might have to go back and adjust this a few times, as it can be hard to figure out where your graph is exactly.
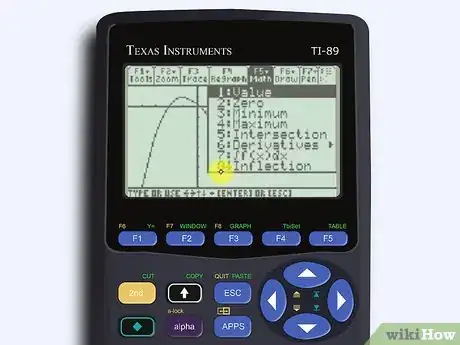
5
Click “Math,” then “Inflection.” Hit the “diamond” or “second” button, then select F5 to open up “Math.” In the dropdown menu, select the option that says “Inflection.”^{[17]
X
Research source}
- This is—you guessed it—how to tell your calculator to calculate inflection points.
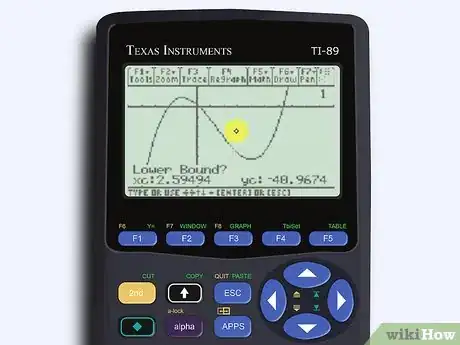
6
Place the cursor on the lower and upper bound of the inflection. Your calculator will give you a message saying “Lower?” Move the arrows on your calculator until the cursor is to the left of the inflection point (you’ll have to know vaguely where it is on the graph). Then, your calculator will ask “Upper?” Move your cursor so it’s to the right of the inflection point, then hit “Enter.”^{[18]
X
Research source}
- This is how you’ll get your calculator to make a guess as to where the inflection point is. Now you have your answer!

Community Q&A

Question

What if the second derivative is a constant? How do I find the inflection point?

Community Answer

Inflection points are where the second derivative changes sign. If it is constant, it never changes sign, so there exists no inflection point for the function.
Question

Can the first derivative become zero at an inflection point?

Orangejews

Community Answer

Yes, for example x^3. It changes concavity at x=0, and the first derivative is 0 there.
Question

Find the value of x at which maximum and minimum values of y and points of inflection occur on the curve y = 12lnx+x^2-10x.

Community Answer

Take the derivative and set it equal to zero, then solve. These are the candidate extrema. Take the second derivative and plug in your results. If it's positive, it's a min; if it's negative, it's a max. Set the second derivative to 0 and solve to find candidate inflection points. We can rule one of them out because of domain restrictions (ln x). Confirm the other by plugging in values around it and checking the sign of the second derivative.