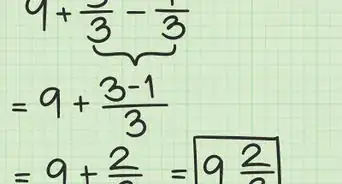X
wikiHow is a “wiki,” similar to Wikipedia, which means that many of our articles are co-written by multiple authors. To create this article, volunteer authors worked to edit and improve it over time.
This article has been viewed 37,387 times.
Learn more...
Absolute value is an expression of a number's distance from 0. It is denoted by two vertical bars on either side of a number, variable, or expression. Anything inside the absolute value bars is called the “argument.” Absolute value bars do not function as parentheses or brackets do, so it is crucial that you use them appropriately.
Steps
Method 1
Method 1 of 2:
Method 1: Simplifying When the Argument Is a Number
-
1Determine your expression. Simplifying a numerical argument is an easy process: because absolute zero represents a distance between your number and 0, your answer will always be positive. Start by performing any operations within the absolute value bars to determine your expression.
- For example, say you are trying to simplify the absolute value of an expression, -6 + 3. Since the entire expression is within the absolute value bars, do the addition first. The problem is now to simplify the absolute value of -3.
-
2Simplify the absolute value. Once you have performed any operations inside the absolute value bars, you can simplify the absolute value. Whatever number you have as your argument, whether positive or negative, represents a distance from 0, so your answer is that number, and it is positive.
- In the example above, the simplified absolute value is 3. This is true because the distance between 0 and -3 is 3.
Advertisement -
3Use a number line. Optionally, you can also note your answer using a number line. This step can help you visualize absolute values and check your work.
- For the example above, your number line should look like this.
Advertisement
Method 2
Method 2 of 2:
Method 2: Simplifying When the Argument Includes a Variable
-
1Deal with an argument that is just a variable. If your argument is just a variable by itself, set equal to a number, then simplifying is very easy. Since absolute value represents a distance from 0, your variable could be either the positive number to which it is equal, or it could be the negative version of that number. There is no way to tell, so include both possibilities in your solution.
- For example, say you know that the absolute value of a variable, x, is equal to 3. You cannot tell if x is positive or negative; you are looking for any number whose distance is 3 from 0. Therefore, you solution is either 3 or -3.
- If this is the kind of argument you need to simplify, stop here. Your work is done. If, however, you have an inequality, continue on.
-
2Recognize absolute value inequalities. If, however, you are given an argument with a variable, expressed as an inequality, more steps are required. Interpret these inequalities as asking you to find all the possible numbers that could work.
- For example, say you have the following inequality.
This can be interpreted as “Show all numbers whose absolute value is less than 7.” In other words, find all numbers whose distance is 7 from 0, excluding 7 itself. Note that the inequality is constructed as “less than” rather than “less than or equal to.” If it were the later, then 7 itself would be included.
- For example, say you have the following inequality.
-
3Graph a number line. The first thing to do, when faced with an absolute value inequality, is to draw a number line. Tag points corresponding with the numbers with which you are working.
- In the example above, your number line would look like this.
The open circles indicate numbers excluded from your final result. Remember: if the inequality were stated as “greater than or equal to” or “less than or equal to,” then these numbers would be included instead. In that case, the circles would be solid.
- In the example above, your number line would look like this.
-
4Consider the numbers on the left side of the number line. Since you don't know whether your variable is positive or negative, you are really dealing with two possible ranges of numbers: those on the left side of the number line and those on the right. First, consider the numbers on the left. Make the variable negative, and convert your absolute value bars to parentheses. Solve.
- In the example above, you would convert the absolute value bars to parentheses to show that (-x) is less than 7. Multiply both sides of the inequality by -1. Note that when you multiply by a negative number, you must switch the inequality sign (from less than to greater than, or vice versa). Your inequality would look like this.
You now know that for the left side of the number line, x will be greater than -7. On a number line, that would look like this.
- In the example above, you would convert the absolute value bars to parentheses to show that (-x) is less than 7. Multiply both sides of the inequality by -1. Note that when you multiply by a negative number, you must switch the inequality sign (from less than to greater than, or vice versa). Your inequality would look like this.
-
5Consider the numbers on the right side of the number line. Now you can look at the other range of numbers, those that are positive. This is even simpler: make the variable positive, convert your absolute value bars to parentheses.
- In the example above, you would convert the absolute value bars to parentheses to show that (x) is less than 7. No further work is necessary for this step. On a number line, that would look like this.
-
6Find the intersect of the two intervals. Once you have considered both sides, you need to determine where the solutions overlap. Draw both intervals on the same number line to get a final result.
- In the example above, you would highlight values greater than -7 and less than 7 (but excluding -7 and 7 themselves). These are your solutions.
Advertisement
Community Q&A
-
QuestionMy paper says to simplify |-15| + |-26|. What do I do?
 DonaganTop AnswererAs the above article explains, |-15| = 15, and |-26| = 26. Your instructions are to add those two values together.
DonaganTop AnswererAs the above article explains, |-15| = 15, and |-26| = 26. Your instructions are to add those two values together. -
QuestionWhat is -2/x-7/, when x is -3?
 DonaganTop AnswererSubstitute (-3) for x: -2 / (-3 -7) = -2 / -10 = 2 / 10 = 1 / 5.
DonaganTop AnswererSubstitute (-3) for x: -2 / (-3 -7) = -2 / -10 = 2 / 10 = 1 / 5. -
QuestionIf I have the expression |sqrt(2) - 1 | -1, how would I simplify it so that there's no absolute values left?
 DonaganTop Answerer|√2 - 1| - 1 = (√2 - 1) - 1 = √2 - 2. You can leave it at that, or insert 1.414 for √2 and subtract 2.
DonaganTop Answerer|√2 - 1| - 1 = (√2 - 1) - 1 = √2 - 2. You can leave it at that, or insert 1.414 for √2 and subtract 2.
Advertisement
References
About This Article
Advertisement
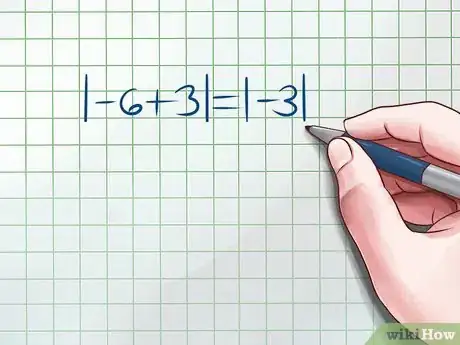
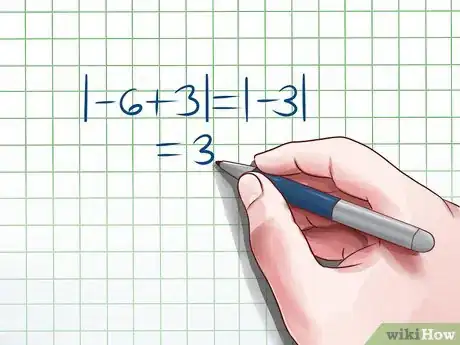
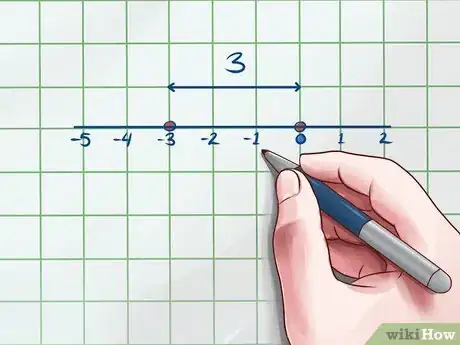



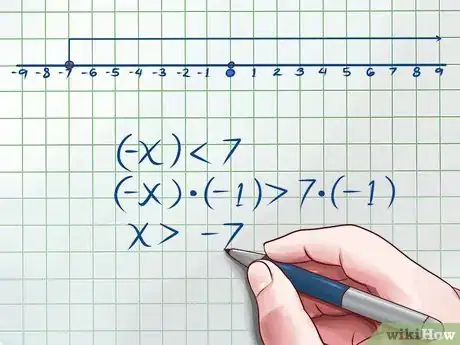

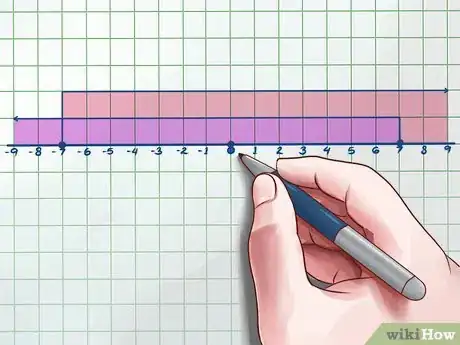









-Step-10-Version-3.webp)