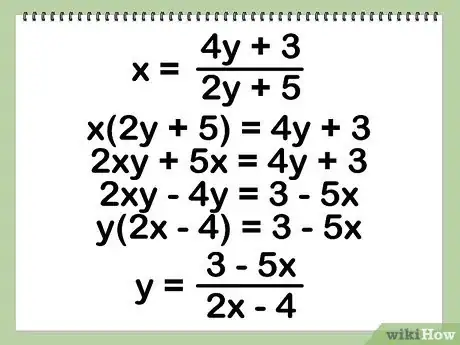wikiHow es un "wiki", lo que significa que muchos de nuestros artículos están escritos por varios autores. Para crear este artículo, autores voluntarios han trabajado para editarlo y mejorarlo con el tiempo.
Este artículo ha sido visto 152 027 veces.
Una parte fundamental en el aprendizaje del álgebra, es aprender cómo encontrar la inversa de una función, o f(x). La inversa de una función es representada por f^-1(x), y es visualmente representada como la función original que se refleja sobre la línea y=x. este artículo te enseñará cómo encontrar la inversa de una función.
Pasos
-
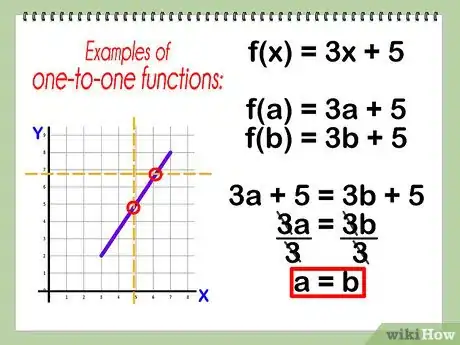
1Asegúrate que tu función sea uno a uno. Solo las funciones uno a uno tienen inversas.
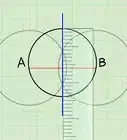
- Una función es uno a uno si pasa la prueba de la línea vertical y la prueba de la línea horizontal. Dibuja una línea vertical a través de toda la gráfica de la función y cuenta el número de veces que la línea toca la función. Después dibuja una línea horizontal a través de toda la gráfica de la función y cuanta el número de veces que esta línea toca la función. Si cada línea solo toca la función una vez, entonces la función es uno-a-uno.
- Si la gráfica no pasa la prueba de la línea vertical, entonces no es una función.
- Para determinar algebraicamente si una función es uno a uno, conecta f(a) y f(b) en tu función y observa si a = b. Como ejemplo, vamos a tomar f(x) = 3x+5.
- f(a) = 3a + 5; f(b) = 3b + 5
- 3a + 5 = 3b + 5
- 3a = 3b
- a = b
- Por lo tanto, f(x) es una función uno-a-uno.
- Una función es uno a uno si pasa la prueba de la línea vertical y la prueba de la línea horizontal. Dibuja una línea vertical a través de toda la gráfica de la función y cuenta el número de veces que la línea toca la función. Después dibuja una línea horizontal a través de toda la gráfica de la función y cuanta el número de veces que esta línea toca la función. Si cada línea solo toca la función una vez, entonces la función es uno-a-uno.
-
2Dada una función, cambia las x y las y. Recuerda que f(x) es un sustituto para "y."
- En una función, "f(x)" o "y", esta representa la salida y "x" representa la entrada. Para encontrar la inversa de la función, debes cambiar las entradas y las salidas.
- Por ejemplo: Tomemos f(x) = (4x+3)/(2x+5) – que es una función uno-a-uno. Si cambiamos las x y las y obtenemos x = (4y + 3)/(2y + 5).
-
3Resuelve para la nueva "y." Necesitarás manipular las expresiones para resolver para y, o para encontrar las nuevas operaciones que deben realizarse en las entradas para obtener la inversa como una salida.
- Esto puede ser complicado dependiendo de tu expresión. Quizás necesites usar algunos trucos algebraicos como la multiplicación cruzada o factorizar para evaluar la expresión y simplificarla.
- En nuestro ejemplo, vamos a realizar estos pasos para aislar y:
- Estamos empezando con x = (4y + 3)/(2y + 5)
- x(2y + 5) = 4y + 3 – Multiplica ambos lados por (2y + 5)
- 2xy + 5x = 4y + 3 –Distribuye las x
- 2xy - 4y = 3 - 5x – Coloca todos los términos en y en un lado
- y(2x - 4) = 3 - 5x – Invierte la distribución para consolidar los términos de y
- y = (3 - 5x)/(2x - 4) – Divide para obtener tu respuesta
-
4Reemplaza la nueva "y" con f^-1(x). Esta es la ecuación de la inversa de tu función original.
- Nuestra respuesta final es f^-1(x) = (3 - 5x)/(2x - 4). Esta es la función inversa de f(x) = (4x+3)/(2x+5).
Anuncio
Referencias
Acerca de este wikiHow
Para encontrar la inversa de una función, primero intercambia las x con las y. Luego simplemente resuelve la ecuación para hallar el valor de la nueva y. Por ejemplo, si la función original era f(x) = (4x+3)/(2x+5), primero intercambia las x con las y para obtener x = (4y+3)/(2y+5). Luego resuelve para hallar el valor de y. Así obtendrás (3-5x)/(2x-4), que es la inversa de la función. ¡Sigue leyendo si quieres aprender a determinar si una función tiene una inversa!