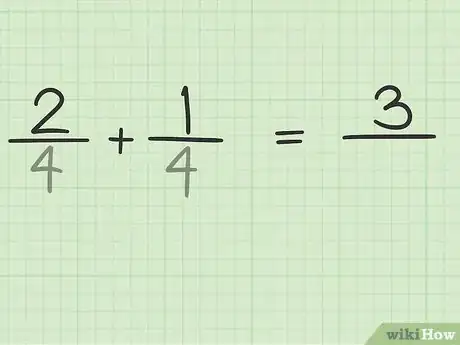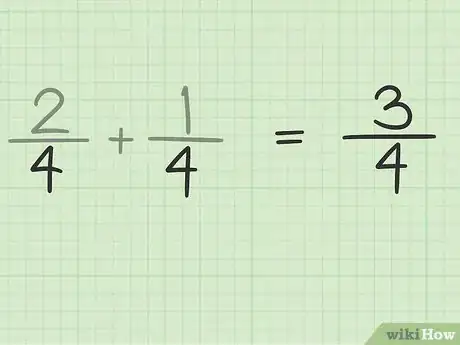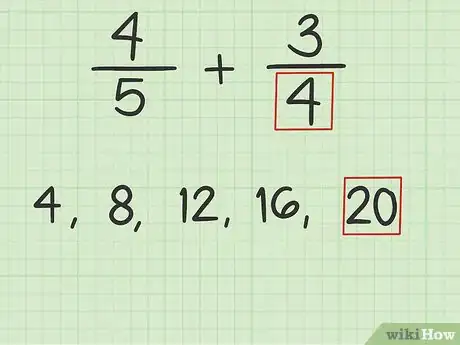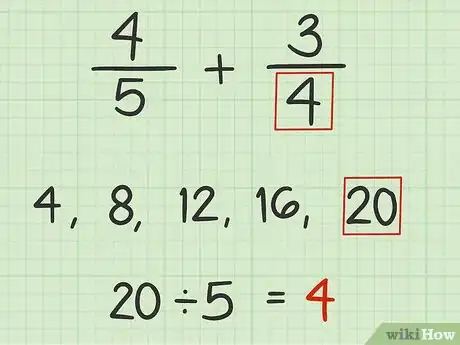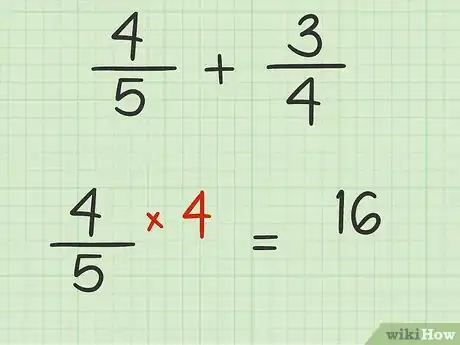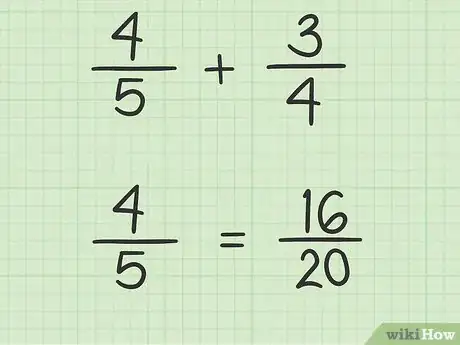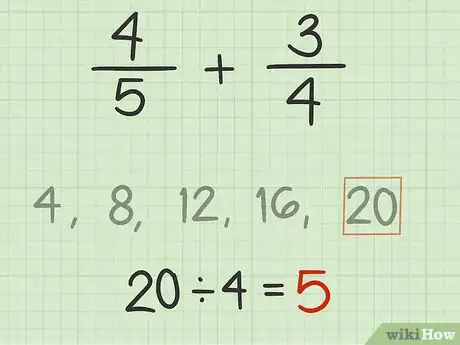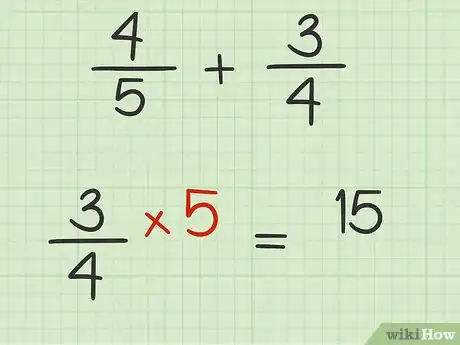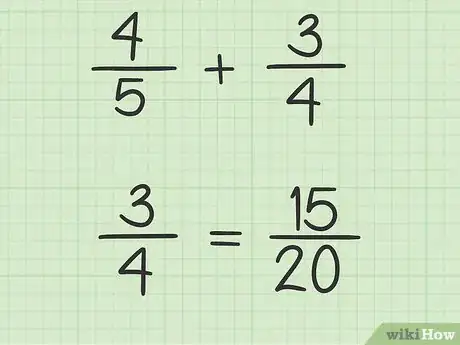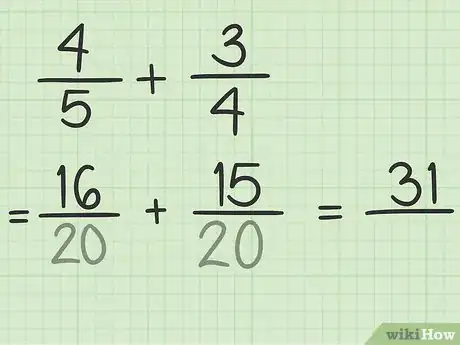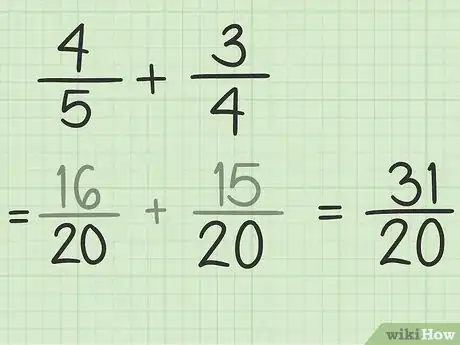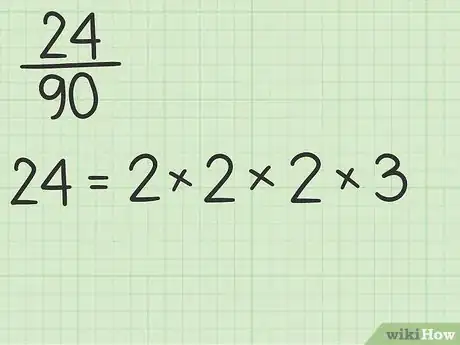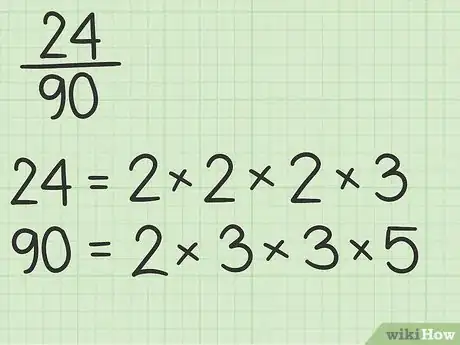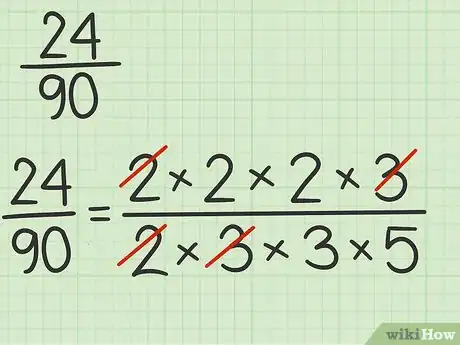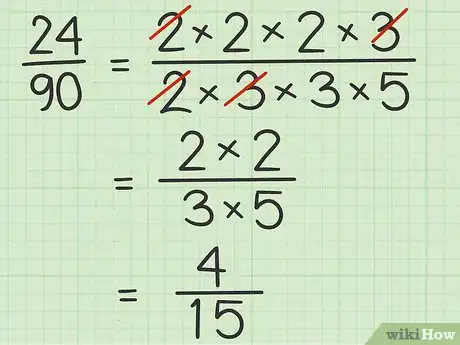Cómo sumar y simplificar fracciones

Coescrito por David Jia

Una vez que comprendas el concepto de fracciones, podrás comenzar a hacer operaciones sencillas con ellas. Puedes sumar fracciones como haces con otros tipos de números. No obstante, lo más importante que debes recordar es que deben tener el mismo denominador antes de sumarlas. Una vez que determines la suma de dos fracciones, probablemente tengas que simplificar o reducir el resultado.

Método 1

Método 1 de 3:
Sumar fracciones con el mismo denominador

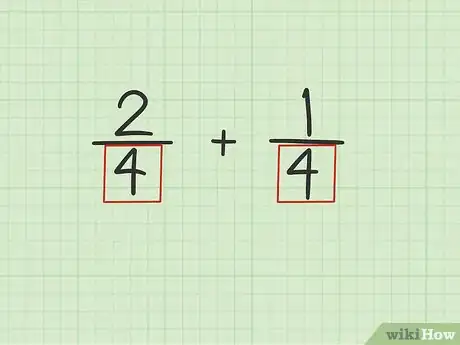
1
Verifica que las fracciones tengan el mismo denominador. El denominador es el número que se sitúa debajo de la línea de fracción.^{[1]
X
Fuente de investigación} Si las fracciones no tienen el mismo denominador, no podrás usar este método.
- Por ejemplo, si vas a calcular ${\frac {2}{4}}+{\frac {1}{4}}$ , notarás que ambas fracciones tienen el mismo denominador: 4.
2
Suma los numeradores. El numerador es el número encima de la línea de fracción. Suma los numeradores como lo harías con los números enteros.^{[2]
X
Fuente de investigación}
- Por ejemplo, los numeradores de ${\frac {2}{4}}$ y ${\frac {1}{4}}$ son 2 y 1, así que la suma sería $2+1=3$ . Por lo tanto, el número 3 es el numerador de la suma.
3
Coloca la suma de los numeradores encima del denominador. Debido a que las dos fracciones que sumarás tienen el mismo denominador, el denominador de su suma también será el mismo.^{[3]
X
Fuente de investigación}
- Por ejemplo, la suma de ${\frac {2}{4}}+{\frac {1}{4}}$ tendrá como denominador el número 4: ${\frac {2}{4}}+{\frac {1}{4}}={\frac {3}{4}}$ .
Anuncio

Método 2

Método 2 de 3:
Sumar fracciones con denominadores diferentes

1
Revisa si las fracciones tienen denominadores diferentes. El denominador es el número que se coloca debajo de la línea de fracción.^{[4]
X
Fuente de investigación}
- Por ejemplo, si vas a sumar ${\frac {4}{5}}+{\frac {3}{4}}$ , notarás que las fracciones tienen denominadores diferentes: 5 y 4.
2
Haz una lista de los primeros múltiplos del denominador más bajo. Un múltiplo es un número entre el que otro número puede dividirse equitativamente. También puedes pensar en un múltiplo como el resultado de multiplicar un número por un número entero. Debes buscar el múltiplo más bajo que los dos denominadores tengan en común.^{[5]
X
Fuente de investigación}
- Por ejemplo, el denominador más bajo en ${\frac {4}{5}}+{\frac {3}{4}}$ es 4. Los primeros múltiplos de 4 son 4, 8, 12, 16 y 20. De estos, el múltiplo más bajo que 5 comparte con 4 es 20. Por lo tanto, 20 es el mínimo común múltiplo de los dos denominadores.
3
Divide el mínimo común múltiplo entre el denominador de la primera fracción. El resultado te dará un factor de cambio. Este factor te dirá cuán alto es el múltiplo común con respecto al denominador .
- Por ejemplo, si el mínimo común múltiplo es 20 y el denominador de la primera fracción es 5, calcularás ${\frac {20}{5}}=4$ . Eso significa que 4 es el factor de cambio. El mínimo común múltiplo es 4 veces mayor que el denominador.
4
Multiplica el numerador de la primera fracción por el factor de cambio. De ese modo, mantendrás una proporción entre el numerador y el denominador de la fracción equivalente.^{[6]
X
Fuente de investigación}
- Por ejemplo, si el factor de cambio es 4 y el numerador de la primera fracción es 4, el cálculo será $4\times 4=16$ .
5
Escribe la fracción equivalente de la primera fracción. El numerador será el producto del factor de cambio y el numerador de la fracción original. El denominador será el mínimo común múltiplo.
- Por ejemplo: ${\frac {4}{5}}={\frac {16}{20}}$ .
6
Divide el mínimo común múltiplo entre el denominador de la segunda fracción. El resultado te dará un factor de cambio para la segunda fracción. Este factor te dirá cuán alto es el múltiplo común en comparación con el denominador.
- Por ejemplo, si el mínimo común múltiplo es 20 y el denominador de la segunda fracción es 4, el cálculo sería ${\frac {20}{4}}=5$ . Eso significa que 5 es el factor de cambio de la segunda fracción.
7
Multiplica el numerador de la segunda fracción por el factor de cambio. De ese modo, obtendrás el numerador de la fracción equivalente.
- Por ejemplo, si el factor de cambio es 5, y el numerador de la segunda fracción es 3, el cálculo será $5\times 3=15$ .
8
Escribe la fracción equivalente de la segunda fracción. El numerador será el producto del factor de cambio y el numerador de la fracción original. El denominador será el mínimo común múltiplo.
- Por ejemplo: ${\frac {3}{4}}={\frac {15}{20}}$ .
9
Suma los numeradores de las fracciones equivalentes. Debido a que las fracciones equivalentes tienen el mismo denominador, puedes sumar los numeradores como lo harías normalmente.^{[7]
X
Fuente de investigación}
- Por ejemplo: $16+15=31$ .
10
Coloca la suma de los numeradores sobre el nuevo denominador. Asegúrate de usar el denominador común de las fracciones equivalentes.^{[8]
X
Fuente de investigación}
- Por ejemplo: ${\frac {16}{20}}+{\frac {15}{20}}={\frac {31}{20}}$ .
Anuncio

Método 3

Método 3 de 3:
Simplificar fracciones

1
Factoriza el numerador. Debes factorizar el numerador en todos sus factores primos. Recuerda que un número primo es aquel que solamente puede dividirse entre sí mismo y el número 1. Vuelve a escribir la fracción mostrando la factorización prima en el numerador.
- Por ejemplo, si vas a simplificar la fracción ${\frac {24}{90}}$ , el cálculo será $24=2\times 2\times 2\times 3$ . Por lo tanto, vuelve a escribirla así: ${\frac {2\times 2\times 2\times 3}{90}}$ .
2
Factoriza el denominador. También debes factorizar el denominador en sus factores primos. Vuelve a escribir la fracción mostrando su factorización prima en el denominador.^{[9]
X
Fuente de investigación}
- Por ejemplo, si vas a simplificar la fracción ${\frac {24}{90}}$ , el resultado será $90=2\times 3\times 3\times 5$ . Por lo tanto, vuelve a escribirla así: ${\frac {2\times 2\times 2\times 3}{2\times 3\times 3\times 5}}$ .
3
Cancela los factores comunes del numerador y denominador. Recuerda que cuando un factor es común a la parte superior e inferior de una fracción, cancela ${\frac {1}{1}}$ ${\frac {1}{1}}$ . Eso significa que puedes eliminar estos factores, ya que cualquier número multiplicado por 1 es igual a sí mismo.^{[10]
X
Fuente de investigación}
- Por ejemplo, puedes cancelar un 2 y un 3 en el numerador y denominador: ${\frac {{\cancel {2\times }}2\times 2{\cancel {\times 3}}}{{\cancel {2\times }}{\cancel {3\times }}3\times 5}}$ .
4
Vuelve a escribir la fracción con los factores restantes. Debes simplificar la fracción, de manera que solamente incluya los factores que no cancelaste. Si más de un factor permanece en el numerador o el denominador, debes multiplicarlos juntos para obtener un solo número entero. El resultado será una fracción simplificada.
- Por ejemplo:
  ${\frac {{\cancel {2\times }}2\times 2{\cancel {\times 3}}}{{\cancel {2\times }}{\cancel {3\times }}3\times 5}}$
  ${\frac {2\times 2}{3\times 5}}$
  ${\frac {4}{15}}$
  Por lo tanto, la fracción ${\frac {24}{90}}$ se simplifica a ${\frac {4}{15}}$ .
Anuncio

Consejos

Sustraer fracciones implica el mismo proceso. Asegúrate de que todas las fracciones tengan el mismo denominador. Luego, resta ambos numeradores y escribe el resultado sobre el denominador común. Finalmente, simplifica o reduce la fracción como lo hiciste anteriormente.

Anuncio