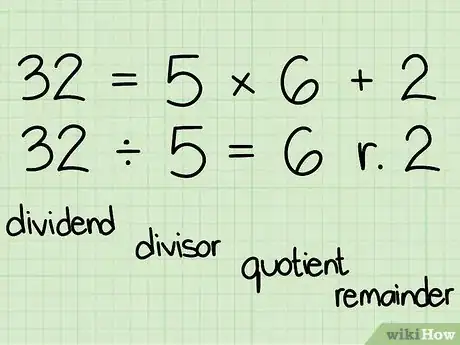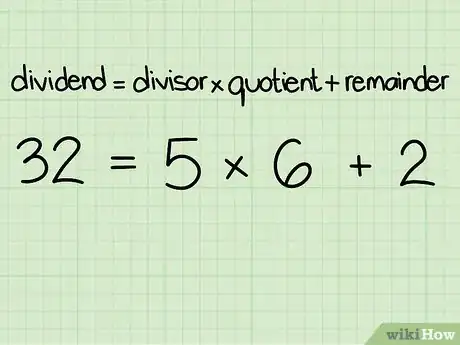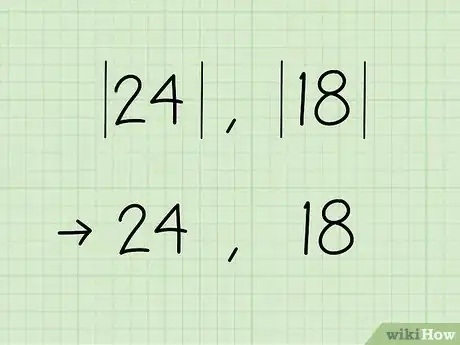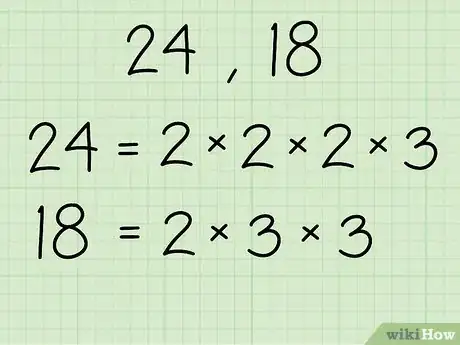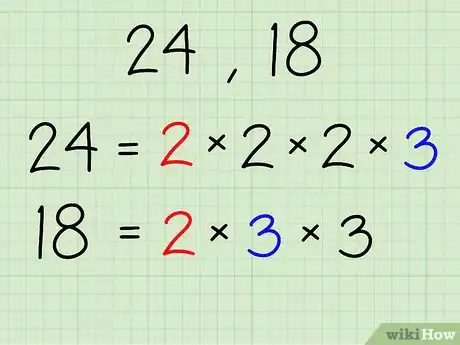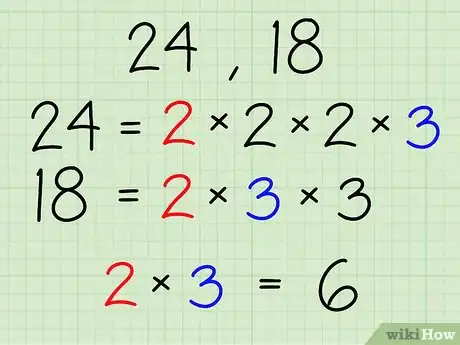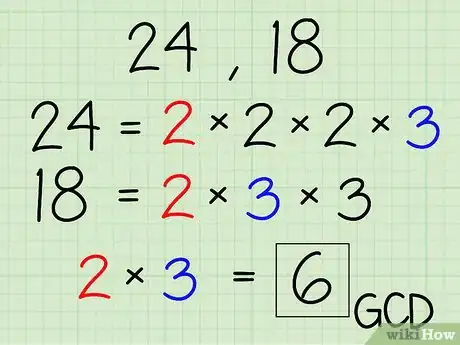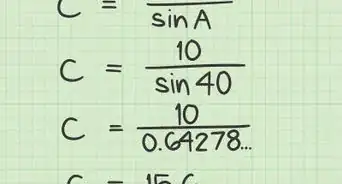Cómo encontrar el máximo común divisor de dos números enteros

Información del autor

El máximo común divisor (MCD) de dos números enteros es el número entero más grande que es un divisor (factor) de ambos. Por ejemplo, el número más largo que divide al 20 y al 16 es el 4. En la escuela, se enseña comúnmente el método de “adivina y revisa”. En lugar de eso, este es una simple y sistemática forma de hacer esto y siempre encontrar la respuesta correcta. Este método se llama “algoritmo de Euclides”. Llamemos a los dos números “a” y “b”.

Método 1

Método 1 de 2:

Utilizar el algoritmo del divisor

1
Deshazte de los números negativos.
2
Aprende tu vocabulario: cuando divides 32 entre 5,
- - 32 es el dividendo
  - 5 es el divisor
  - 6 es el cociente
  - 2 es el residuo.
3
Identifica el número más grande de los dos. Ese será el dividendo, y el más pequeño el divisor.
4
Escribe este algoritmo: (dividendo) = (divisor) * (cociente) + (residuo)
5
Pon el número más grande en el lugar del dividendo, y el número más pequeño como el divisor.
6
Decide cuantas veces el número pequeño cabe en el número grande, y pon ese algoritmo como el cociente.
7
Calcula el residuo, sustitúyelo en el lugar apropiado en el algoritmo.
8
Escribe el algoritmo de nuevo, pero ahora A) úsa el divisor anterior como el dividendo y B) usa el residuo como el nuevo divisor.
9
Repite los pasos hasta que el residuo sea cero.
10
El ultimo divisor es máximo común divisor.
11
Aquí hay un ejemplo, donde estamos tratando de encontrar el máximo común divisor de 108 y 30:
12
Nota como el 30 y el 18 cambian de posición en la segunda línea. Luego, el 18 y el 12 en la tercera línea, y el 12 y el 6 en la cuarta línea. El 3, 1, 1, y 2 que siguen después del símbolo de multiplicación no reaparecen. Representan cuantas veces el divisor cabe en el dividendo, así que son únicos en cada línea.

Anuncio

Método 2

Método 2 de 2:

Utilizar factores primos

1
Elimina cualquier signo negativo.
2
Encuentra los factores primos de los números, y en lístalos como se muestra a continuación.
- Usando 24 y 18 como ejemplo:
  - 24- 2 x 2 x 2 x 3
  - 18- 2 x 3 x 3
- Usando 50 y 35 como ejemplo:
  - 50- 2 x 5 x 5
  - 35- 5 x 7
3
Identifica todos los factores primos comunes.
- Usando 24 y 18 como ejemplo:
  - 24- 2 x 2 x 2 x 3
  - 18- 2 x 3 x 3
- Usando 50 y 35 como ejemplo:
  - 50- 2 x 5 x 5
  - 35- 5 x 7
4
Multiplica los factores comunes juntos.
- En el caso de 24 y 18, multiplica el 2 y 3 para obtener 6. El 6 es máximo común divisor de 24 y 18.
- En el caso de 50 y 35, no hay nada que multiplicar. 5 es el único factor común, y por lo tanto es el más grande.
5
Terminado.

Anuncio

Consejos

Una forma de escribir esto, usando la notación <dividendo> mod <divisor> = el residuo es ese MCD(a,b) = b si a mod b = 0, y MCD(a,b) = GCD(b, a mod b) de otra manera.
Como, encontremos el MCD (-77,91).Primero usemos 77 en lugar de -77, so MCD(-77,91) se convierte en MCD(77,91). Ahora, 77 es menos que 91, así que hay que cambiarlo, Pero veamos cómo se encarga de eso el algoritmo si no lo hacemos. Cuando calculamos 77 y 91, obtenemos 77 (ya que 77 = 91 x 0 + 77). Ya que eso no es un cero, cambiamos (a, b) por (b, a mod b) y eso nos da: MCD(77,91) = MCD(91,77). 91 mod 77 da 14 (recuerda, eso significa que 14 es el residuo). Ya que no es cero, cambiamos MCD(91,77) por MCD(77,14). 77 mod 14 da 7 lo cual no es cero, así que cambiamos MCD(77,14) por MCD(14,7). 14 mod 7 es cero, ya que 14 = 7 * 2 sin residuo, así que paramos. Y eso significa que: MCD(-77,91) = 7.
Esta técnica es muy útil cuando quieres simplificar fracciones. Por el ejemplo anterior, la fracción -77/91 se reduce a -11/13 porque 7 es el MCD de -77 y 91.
Si 'a' y 'b' son ambos cero, entonces cualquier número que no sea cero los divide a ambos, así que técnicamente no hay ningún MCD en este caso. Los matemáticos a menudo dicen que el MCD de 0 y 0 es 0, y esa es la respuesta que este método obtiene.

Anuncio