Nuestro equipo de editores e investigadores capacitados han sido autores de este artículo y lo han validado por su precisión y amplitud.
El equipo de contenido de wikiHow revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad.
En este artículo, hay 7 referencias citadas, que se pueden ver en la parte inferior de la página.
Este artículo ha sido visto 263 446 veces.
Una diagonal es una línea recta que conecta una esquina de un rectángulo con la esquina opuesta.[1] Un rectángulo tiene dos diagonales, cada una de la misma longitud.[2] Si conoces la longitud de los lados del rectángulo, puedes encontrar fácilmente la longitud de la diagonal usando el teorema de Pitágoras, ya que una diagonal divide un rectángulo en dos triángulos rectángulos. Si no conoces la longitud de los lados, pero tienes otra información, como el área y el perímetro o la relación entre la longitud de los lados, puedes seguir unos pasos adicionales para encontrar la longitud y el ancho del rectángulo y, a partir de allí, puedes usar el teorema de Pitágoras para encontrar la longitud de la diagonal.
Pasos
Usar la longitud y el ancho del rectángulo
-
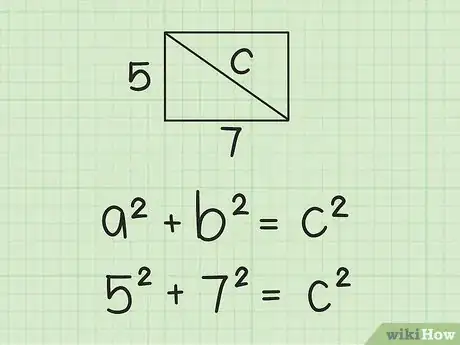
1Determina la fórmula para el teorema de Pitágoras. La fórmula es , donde y son iguales a la longitud de cada lado de un triángulo rectángulo y es igual a la longitud de la hipotenusa de este triángulo.[3]
- Usarás el teorema de Pitágoras porque la diagonal de un rectángulo lo divide en dos triángulos rectángulos congruentes.[4] La longitud y el ancho del rectángulo son los lados del triángulo y la diagonal es la hipotenusa.
-
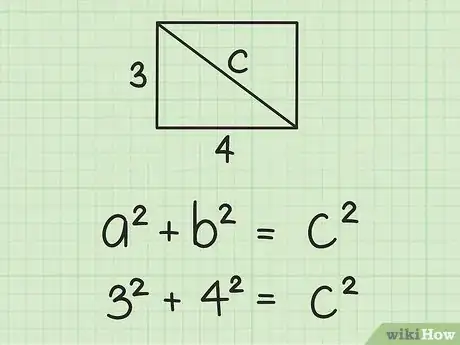
2Reemplaza la longitud y el ancho en la fórmula. Se te debería dar estos valores o deberías poder medirlos. Asegúrate de reemplazar y ..
- Por ejemplo, si el ancho de un rectángulo mide 3 cm y la longitud mide 4 cm, la fórmula se verá así: .
-
3Eleva la longitud y el ancho al cuadrado y luego suma estos resultados. Recuerda: elevar un número al cuadrado significa multiplicarlo por sí mismo.
- Por ejemplo:
- Por ejemplo:
-
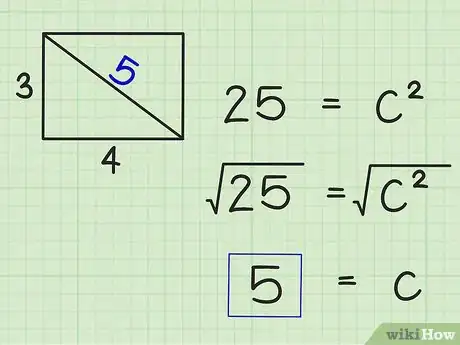
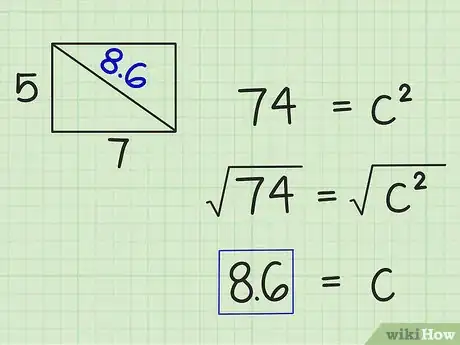
4Saca la raíz cuadrada de cada lado de la ecuación. La forma más fácil de encontrar una raíz cuadrada es usar una calculadora. Puedes usar una calculadora en línea si no tienes una calculadora científica.[5] Esto te dará el valor de , el cual es la hipotenusa del triángulo y la diagonal del rectángulo.
- Por ejemplo:
Entonces, la diagonal de un rectángulo con un ancho de 3 cm y una longitud de 4 cm mide 5 cm.
Anuncio - Por ejemplo:
Usar el área y el perímetro
-
1Determina la fórmula para el área de un rectángulo. La fórmula es , donde es igual al área del rectángulo, es igual a la longitud del rectángulo y es igual al ancho del rectángulo (por sus siglas en inglés).[6]
-
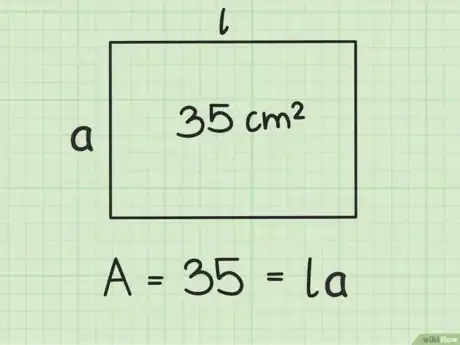
2Reemplaza el área del rectángulo en la fórmula. Asegúrate de reemplazar la variable .
- Por ejemplo, si el área del rectángulo mide 35 centímetros cuadrados, la fórmula se verá así: .
-
3Reordena la fórmula para encontrar el valor de . Para hacerlo, divide ambos lados de la ecuación entre . Haz a un lado este valor. Lo reemplazarás en la fórmula del perímetro más adelante.
- Por ejemplo:
- Por ejemplo:
-
4Determina la fórmula para el perímetro de un rectángulo. La fórmula es , donde es igual al ancho del rectángulo y es igual a la longitud.[7]
-
5Reemplaza el valor del perímetro en la fórmula. Asegúrate de reemplazar la variable .
- Por ejemplo, si el perímetro de un rectángulo mide 24 cm, la fórmula se verá así: .
-
6Divide ambos lados de la ecuación entre 2. Esto te dará el valor de .
- Por ejemplo:
- Por ejemplo:
-
7Reemplaza el valor de en la ecuación. Usa el valor que encontraste al reordenar la fórmula para el área.
- Por ejemplo, si, al usar la fórmula para el área, encontraste que , reemplaza este valor de en la fórmula para el perímetro:
.
- Por ejemplo, si, al usar la fórmula para el área, encontraste que , reemplaza este valor de en la fórmula para el perímetro:
-
8Cancela la fracción en la ecuación. Para hacerlo, multiplica ambos lados de la ecuación por .
- Por ejemplo:
- Por ejemplo:
-
9Establece un valor de 0 para la ecuación. Para hacerlo, resta el término de primer grado a ambos lados de la ecuación.
- Por ejemplo:
- Por ejemplo:
-
10Reorganiza la ecuación según el orden de los términos. Esto quiere decir que el término con el exponente irá primero, seguido del término con la variable y luego de la constante. Al reordenar, asegúrate de mantener los signos negativos y positivos correctos. Ten en cuenta que la ecuación ahora está organizada como una ecuación cuadrática.
- Por ejemplo: se convierte en .
-
11Factoriza la ecuación cuadrática. Para obtener instrucciones completas sobre cómo hacerlo, lee el artículo "Cómo resolver ecuaciones cuadráticas".
- Por ejemplo, la ecuación puede factorizarse como .
-
12Encuentra los valores de . Para hacerlo, establece cada uno como igual a cero y resuelve la ecuación para encontrar la variable. Encontrarás dos soluciones o raíces para la ecuación. Ya que tienes un rectángulo, las raíces serán la longitud y el ancho del rectángulo.
- Por ejemplo:
Y
Por lo tanto, la longitud y el ancho del rectángulo miden 7 y 5 cm, respectivamente.
- Por ejemplo:
-
13Determina la fórmula para el teorema de Pitágoras , donde y son iguales a la longitud de cada lado de un triángulo rectángulo y es igual a la longitud de la hipotenusa.[8]
- Usarás el teorema de Pitágoras porque la diagonal de un rectángulo lo divide en dos triángulos rectángulos congruentes.[9] El ancho y la longitud del rectángulo son los lados del triángulo y la diagonal es la hipotenusa del triángulo.
-
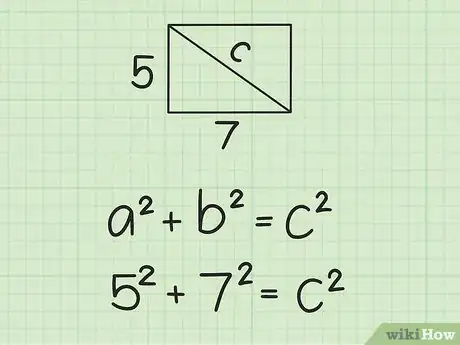
14Reemplaza el ancho y la longitud en la fórmula. No importa qué valor uses para cada variable.
- Por ejemplo, si encuentras que el ancho y la longitud del rectángulo miden 5 y 7 cm, respectivamente, la fórmula se verá así: .
-
15Eleva el ancho y la longitud al cuadrado y luego suma estos números. Recuerda: elevar un número al cuadrado significa multiplicarlo por sí mismo.
- Por ejemplo:
- Por ejemplo:
-
16Saca la raíz cuadrada de cada lado de la ecuación. La forma más fácil de encontrar una raíz cuadrada es usar una calculadora. Puedes usar una calculadora en línea si no tienes una calculadora científica.[10] Esto te dará el valor de , el cual es la hipotenusa del triángulo y la diagonal del rectángulo.
- Por ejemplo:
Entonces, la diagonal de un rectángulo con un área de 35 centímetros cuadrados y un perímetro de 24 cm mide alrededor de 8,6 cm.
Anuncio - Por ejemplo:
Usar el área y las relaciones entre la longitud de cada lado
-
1Escribe una fórmula que explique la relación entre la longitud de cada lado del rectángulo.[11] Puedes aislar la longitud () o el ancho (). Reemplaza esta fórmula ya que la reemplazarás más adelante en la fórmula para el área.
- Por ejemplo, si sabes que el ancho de un rectángulo mide 2 cm más que la longitud, puedes escribir una fórmula para : .
-
2Determina la fórmula para el área de un rectángulo. La fórmula es , donde es igual al área del rectángulo, es igual a la longitud del rectángulo y es igual al ancho del rectángulo.[12]
- Puedes usar este método si conoces el perímetro del rectángulo, excepto que determinarías la fórmula para el perímetro en lugar de la fórmula para el área. La fórmula para el perímetro de un rectángulo es , donde es igual al ancho del rectángulo y es igual a la longitud del rectángulo.[13]
-
3Reemplaza el área del rectángulo en la fórmula. Asegúrate de reemplazar la variable .
- Por ejemplo, si el área del rectángulo mide 35 centímetros cuadrados, la fórmula se verá así: .
-
4Reemplaza la fórmula relacional para la longitud (o el ancho) en la fórmula para el área. Ya que estás trabajando con un rectángulo, no importa si trabajas con la variable o .
- Por ejemplo, si encuentras que , reemplaza esta relación por en la fórmula para el área:
- Por ejemplo, si encuentras que , reemplaza esta relación por en la fórmula para el área:
-
5Establece una ecuación cuadrática. Para hacerlo, usa la propiedad distributiva para multiplicar los términos entre paréntesis y luego establecer el valor de la ecuación como 0.
- Por ejemplo:
- Por ejemplo:
-
6Factoriza la ecuación cuadrática. Para obtener instrucciones completas sobre cómo hacerlo, lee el artículo "Cómo resolver ecuaciones cuadráticas".
- Por ejemplo, la ecuación puede factorizarse como .
-
7Encuentra los valores de . Para hacerlo, establece cada término como igual a cero y resuelve para encontrar el valor de la variable. Encontrarás dos soluciones o raíces para la ecuación.
- Por ejemplo:
Y
En este caso, tienes una raíz negativa. Debido a que la longitud de un rectángulo no puede ser negativa, sabrás que la longitud debe ser 5 cm.
- Por ejemplo:
-
8Reemplaza el valor de la longitud (o el ancho) en la fórmula relacional. Esto te dará la longitud del otro lado del rectángulo.
- Por ejemplo, si sabes que la longitud del rectángulo mide 5 cm y que la relación entre la longitud de cada lado es , reemplaza 5 por la longitud en la fórmula:
- Por ejemplo, si sabes que la longitud del rectángulo mide 5 cm y que la relación entre la longitud de cada lado es , reemplaza 5 por la longitud en la fórmula:
-
9Determina la fórmula para el teorema de Pitágoras. La fórmula es , donde y son iguales a la longitud de cada lado de un triángulo rectángulo y es igual a la longitud de su hipotenusa.[14]
- Usarás el teorema de Pitágoras porque la diagonal de un rectángulo lo divide en dos triángulos rectángulos congruentes.[15] El ancho y la longitud del rectángulo son los lados del triángulo y la diagonal es la hipotenusa del triángulo.
-
10Reemplaza el ancho y la longitud en la fórmula. No importa qué valor uses para cada variable.
- Por ejemplo, si encontraste que el ancho y la longitud del rectángulo miden 5 y 7 cm, respectivamente, la fórmula se verá así: .
-
11Eleva el ancho y la longitud al cuadrado y luego suma estos números. Recuerda: elevar un número al cuadrado significa multiplicarlo por sí mismo.
- Por ejemplo:
- Por ejemplo:
-
12Saca la raíz cuadrada de cada lado de la ecuación. La forma más fácil de encontrar una raíz cuadrada es usar una calculadora. Puedes usar una calculadora en línea si no tienes una calculadora científica.[16] Esto te dará el valor de , el cual es la hipotenusa del triángulo y la diagonal del rectángulo.
- Por ejemplo:
Entonces, la diagonal de un rectángulo con un ancho que mida 2 cm más que la longitud y un área de 35 centímetros cuadrados mide alrededor de 8,6 cm.
Anuncio - Por ejemplo:
Referencias
- ↑ http://www.mathopenref.com/rectanglediagonals.html
- ↑ http://www.mathwarehouse.com/geometry/quadrilaterals/parallelograms/rectangle.php
- ↑ http://mathworld.wolfram.com/PythagoreanTheorem.html
- ↑ http://www.mathopenref.com/rectanglediagonals.html
- ↑ https://support.google.com/websearch/answer/3284611?hl=en
- ↑ http://www.mathopenref.com/rectanglearea.html
- ↑ http://www.mathopenref.com/rectangleperimeter.html
- ↑ http://mathworld.wolfram.com/PythagoreanTheorem.html
- ↑ http://www.mathopenref.com/rectanglediagonals.html
- ↑ https://support.google.com/websearch/answer/3284611?hl=en
- ↑ http://www.algebralab.org/Word/Word.aspx?file=Geometry_AreaPerimeterRectangles.xml
- ↑ http://www.mathopenref.com/rectanglearea.html
- ↑ http://www.mathopenref.com/rectangleperimeter.html
- ↑ http://mathworld.wolfram.com/PythagoreanTheorem.html
- ↑ http://www.mathopenref.com/rectanglediagonals.html
- ↑ https://support.google.com/websearch/answer/3284611?hl=en




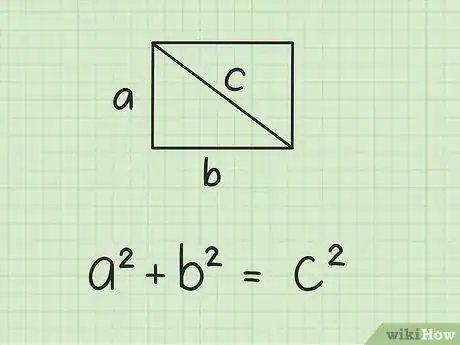





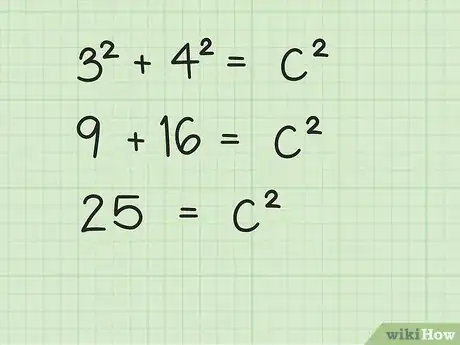




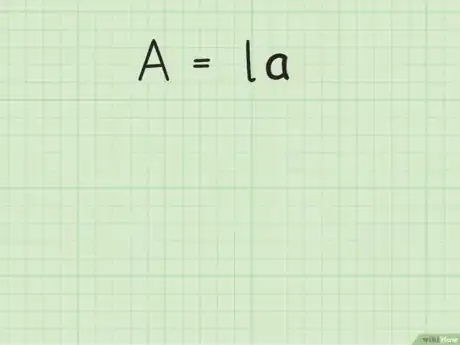






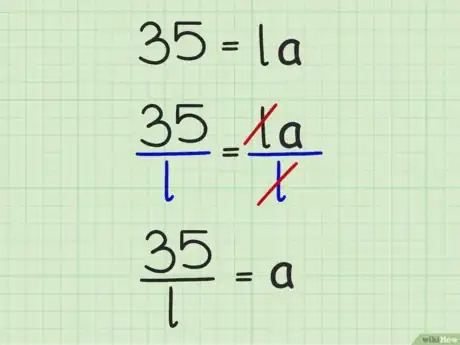

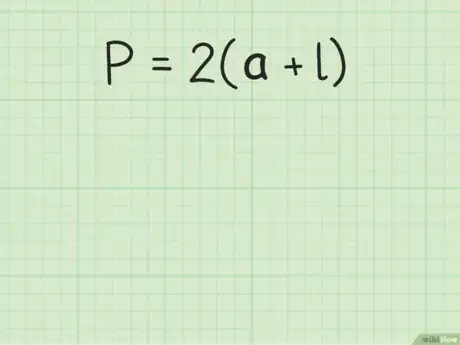




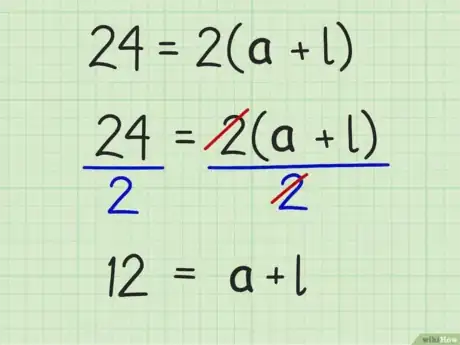



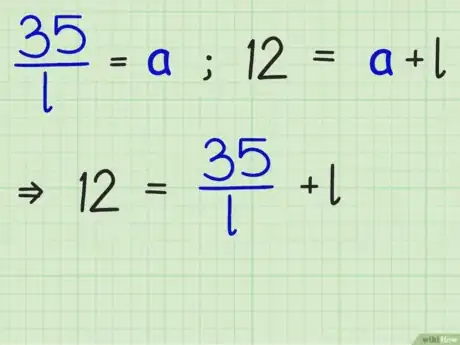

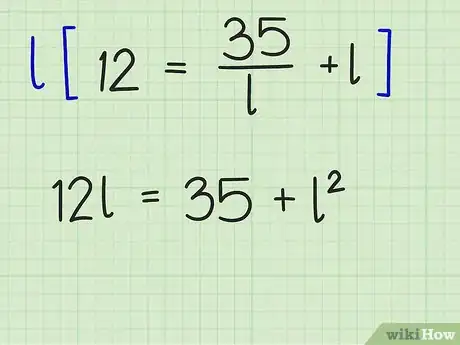







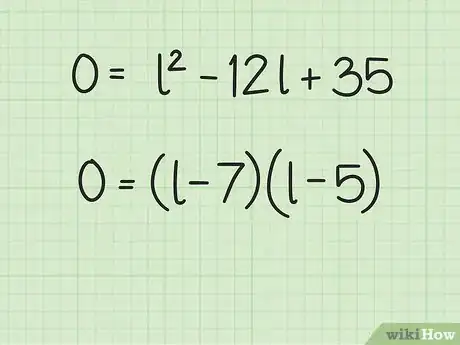






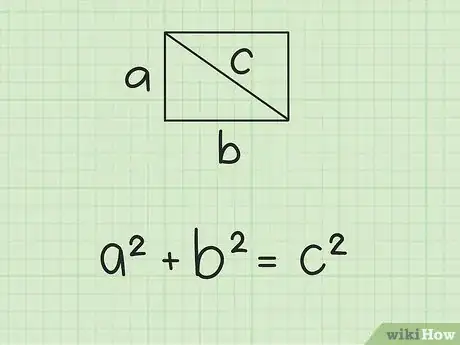

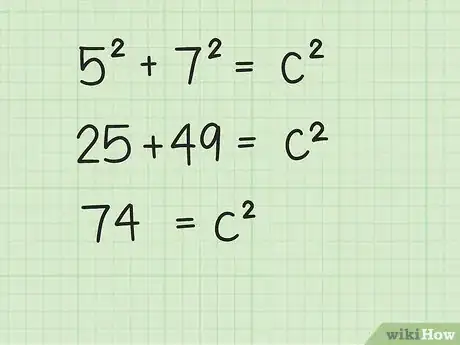




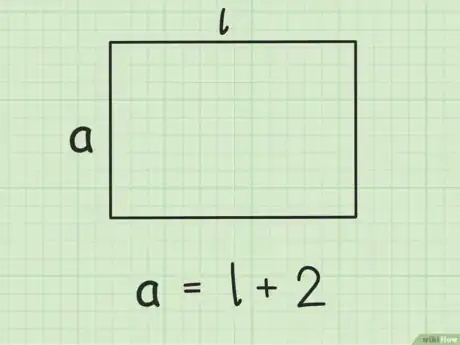

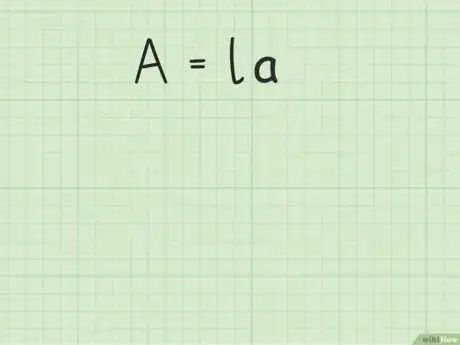
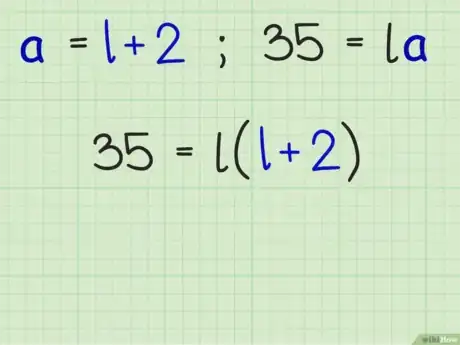

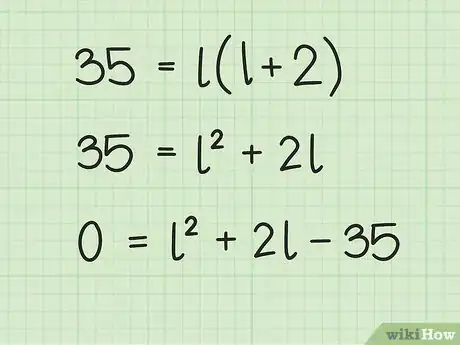


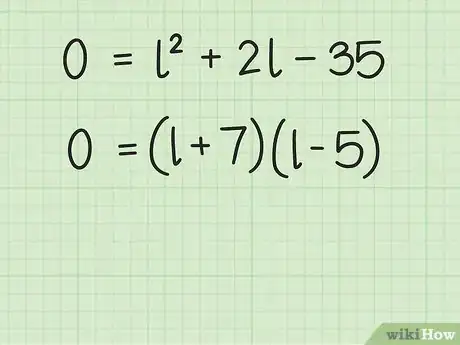




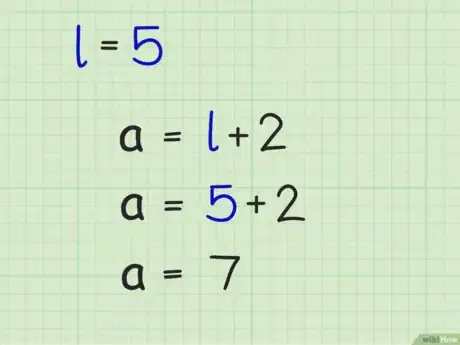


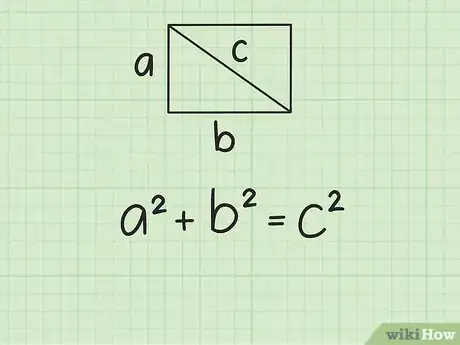
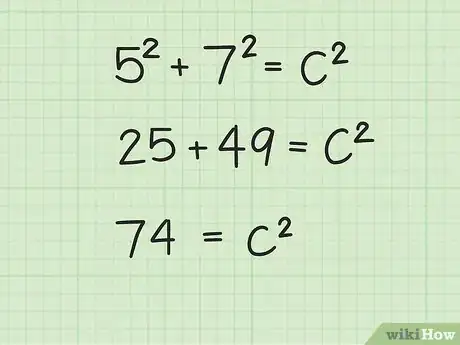














El equipo de contenido de wikiHow revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad. Este artículo ha sido visto 263 446 veces.