Hexagonal pyramid
In geometry, a hexagonal pyramid or hexacone is a pyramid with a hexagonal base upon which are erected six isosceles triangular faces that meet at a point (the apex). Like any pyramid, it is self-dual.
| Hexagonal pyramid | |
|---|---|
 | |
| Type | Pyramid |
| Faces | 6 triangles 1 hexagon |
| Edges | 12 |
| Vertices | 7 |
| Vertex configuration | 6(32.6) (36) |
| Schläfli symbol | ( ) ∨ {6} |
| Symmetry group | C6v, [6], (*66) |
| Rotation group | C6, [6]+, (66) |
| Dual polyhedron | Self-dual |
| Properties | Convex |
| Net | |
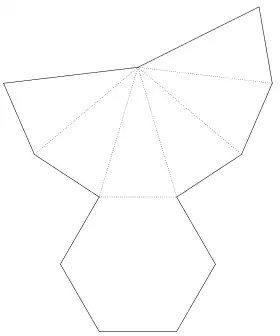 | |
A right hexagonal pyramid with a regular hexagon base has C6v symmetry.
A right regular pyramid is one which has a regular polygon as its base and whose apex is "above" the center of the base, so that the apex, the center of the base and any other vertex form a right triangle.
Vertex coordinates
A hexagonal pyramid of edge length 1 has the following vertices:
These coordinates are a subset of the vertices of the regular triangular tiling.
Representations
STL Hexagonal pyramid

A hexagonal pyramid has the following Coxeter diagrams:
- ox6oo&#x (full symmetry)
- ox3ox&#x (generally a ditrigonal pyramid)
Related polyhedra
| Regular pyramids | ||||||||
|---|---|---|---|---|---|---|---|---|
| Digonal | Triangular | Square | Pentagonal | Hexagonal | Heptagonal | Octagonal | Enneagonal | Decagonal... |
| Improper | Regular | Equilateral | Isosceles | |||||
 |
 |
 |
 | |||||
 |
 |
 |
 |
 |
 |
 |
 | |
External links
- Weisstein, Eric W. "Hexagonal Pyramid". MathWorld.
- Virtual Reality Polyhedra www.georgehart.com: The Encyclopedia of Polyhedra
- Conway Notation for Polyhedra Try: "Y6"
- Hexagonal pyramid - Polytope Wiki
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.