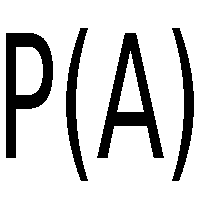Conjunto potencia
| ||||||
Conjunto potencia. En Matemática, Lógica y Matemática Discreta, dícese de la operación conjuntual que obtiene, a partir de un conjunto dado como parámetro, otro conjunto conformado por exactamente todos los subconjuntos de aquel.
En cualquier caso su representación puede ser P(A), ![]()
![]()
El conjunto potencia, sobre todo de conjuntos finitos, tiene gran uso en la modelación de fenómenos y en las definiciones de conceptos y propiedades de figuras matemáticas o de otras ramas de la ciencia.
Definición
Sea un conjunto A, se le llama conjunto potencia de A y se denota P(A), ![]()
![]()
Propiedades
Sea A un conjunto y P(A) su correspondiente conjunto potencia entonces se cumple:
- Si A es un conjunto finito tal que |A|=n entonces |P(A)|=2n.
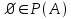
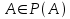
- Si

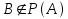
- Si
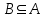
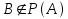
- Todos los elementos de P(A) son conjuntos.
- Si A={} entonces P(A)={{}}.
Algoritmo de construcción de subconjuntos
Sea un conjunto finito A de tamaño n pueden obtenerse todos sus subconjuntos mediante el método combinatorio:
- P = {{}} (el conjunto vacío siempre es subconjunto de cualquier conjunto).
- Se enumeran los elementos de A={a1,a2,...,an}
- Para cada i en el rango natural [1,2n]:
- S={}
- Para cada j en el rango [1,n]:
- Si i & 2j==2j (bitwise AND) (Si está la posición j-ésima marcada en i):
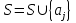
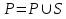
Al concluir P contiene el conjunto potencia de A.
Ejemplos
- A={}, P(A)={{}}.
- A={a}, P(A)={{},{a}}
- A={a,b},P(A)={{}, {a}, {b}, {a,b}}
- C={v,w,x,y,z}, |PC|=32
- Sea P el conjunto de los naturales pares,
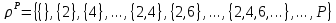
Importancia
El conjunto potencia, sobre todo de conjuntos finitos, tiene gran uso en la modelación de fenómenos y en las definiciones de conceptos y propiedades de figuras matemáticas o de otras ramas de la ciencia.
Por solo mencionar un caso, el proceso de transformación de autómata finito no determinista en autómata finito determinista se realiza mediante el método de construcción de subconjuntos (excepto el conjunto vacío), con la eliminación posterior de los elementos inaccesibles desde el estado inicial según la clausura de Kleene, resultando en un AFD.
Fuentes
- K. Ribnikov. Análisis Combinatorio. Editorial Mir. Moscú, 1988.
- I. Bronshtein, K. Semendiaev. Manual de Matemáticas para ingenieros y estudiantes. 2da Edición. Editorial Mir. Moscú, 1973.
- Página del Coeficiente binomial en Wikipedia. Consultado el 1 de diciembre de 2013.
- Conjunto en Wikipedia. Consultado el 1 de diciembre de 2013.