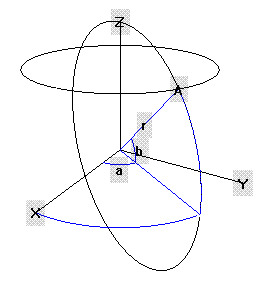
Coordenada esférica

Coordenadas esféricas
Concepto:Forma de expresar la localización de un punto cualquiera de la superficie de una esfera.

Coordenadas esféricas. En Matemáticas y más específicamente, Geometría Analítica, dícese de la forma de identificar un punto en el espacio tridimensional colocado en la superficie de una esfera con centro en el origen y radio determinado mediante tres magnitudes: una distancia y dos ángulos o (r,a,b) donde r, el radio de la esfera; a, la longitud y la latitud es b ambos últimos expresados en radianes de forma parecida a como se hace con las coordenadas terrestres.

Por lo general, suele obviarse el radio ya que éste suele definirse de antemano, dejando solo las otras dimensiones para caracterizar el punto en cuestión.

La relación con la ubicación de puntos relativos por ejemplo a la superficie terrestre es evidente, siendo vital en la geografía y la navegación, así como de estrellas y otros cuerpos celestes desde la perspectiva de la Tierra.

Definición


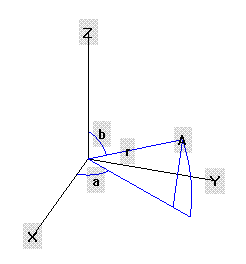
Todo punto A en el espacio tridimensional puede definirse mediante tres dimensiones (en la imagen se identifica con la terna (r,a,b)):

  1. Una distancia radial r donde .
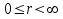
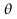
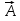
  2. Longitud (a en la figura): La amplitud en radianes del ángulo XOAx, en sentido antihorario, donde Ax es la proyección del vector en el plano XOY.
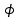
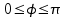
  3. Latitud (b en la figura): La amplitud en radianes del ángulo ZOA, .

A esta forma de definir la posición de A se denomina coordenadas esféricas de A.

Es muy común convenir previamente el radio y reducir las coordenadas solo a los ángulos longitudinales y latitudinales, de forma que la mayoría de las veces se expresa la coordenada de un punto de la forma .

A las circunferencias definidas de fijar el radio y la latitud se les conoce como paralelos, cuyos planos son paralelos a XOY y a las circunferencias verticales definidas al dejar constantes las magnitudes del radio y la longitud se les llama meridianos.

Importancia

Aparte de la evidente relación con el sistema de coordenadas geográficas, aplicables a otros planetas y cuerpos espaciales con forma esférica y el sistema de localización polar de los cuerpos estelares en la bóveda celeste, el sistema de ubicación GPS; desde el punto de vista de la geometría analítica y la precisión realista de los fenómenos que suceden en la superficie terrestre, donde la línea recta es apenas un ideal geométrico, gana gran importancia para las ciencias de la naturaleza y las propiedades espaciales de la trigonometría, especialmente la trigonometría esférica, donde por solo citar un ejemplo los triángulos formados por líneas geodésicas no necesariamente la suma de sus ángulos interiores es 1800.

Relaciones con otros sistemas de coordenadas

A continuación se exponen las particularidades de traslado, semejanzas y diferencias con otros sistemas de coordenadas espaciales.

Coordenadas geográficas

Pese a la similitud evidente entre la caracterización de un punto según sus coordenadas esféricas y geográficas, la diferencia fundamental radica en la forma de definir la latitud que si bien en las coordenadas esféricas se define por el ángulo entre el eje Z y el vector ; en el caso de la latitud geográfica se define mediante el ángulo formado por el propio vector y la proyección del mismo sobre el plano XOY:

Coordenadas cartesianas

Las fórmulas de conversión entre los sistemas esféricos y cartesianos son simples. Dada la coordenada esférica (r,a,b) su equivalente cartesiano (x,y,z) vendría dado por la relación:

  • x=r cos a cos b
  • y=r sen a cos b
  • z=r cos b

Coordenadas cilíndricas

Si bien las coordenadas esféricas (r,a,b) y cilíndricas (a,R,z) tiene como elemento común el ángulo longitudinal a conformado entre el eje X el origen de coordenadas y la proyección del vector A sobre el plano XOY; aunque difiere en el hecho de que el radio R de la base del cilindro es el módulo del vector proyectado y no como en el sistema esférico, donde el radio r era la distanciaOA.


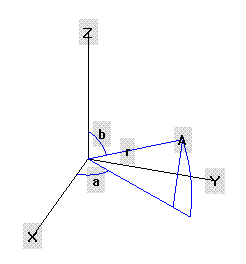
Por ende, las coordenadas esféricas y las cilíndricas se relacionan mediante las fórmulas:

  • r2=z2+R2

Veáse también

Fuentes

This article is issued from Ecured. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.