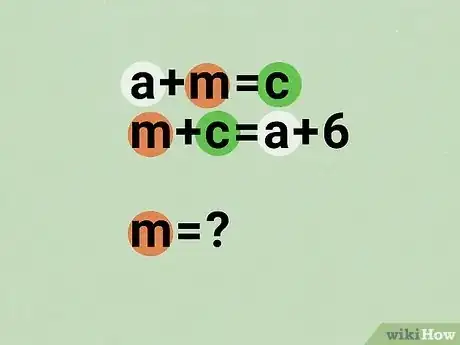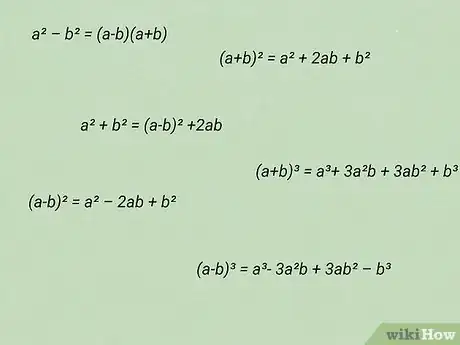Cómo resolver problemas de matemáticas

Coescrito por Daron Cam

Aunque los problemas de matemáticas se pueden resolver de diferentes maneras, existe un método general de visualizar, plantear y resolver los problemas de matemáticas que puede ayudarte a resolver incluso el problema más difícil. Usar estas estrategias también puede ayudarte a mejorar tus habilidades matemáticas en general. Sigue leyendo para aprender sobre algunas de estas estrategias para resolver problemas matemáticos.

Parte 1

Parte 1 de 3:
Comprender el problema

$Imagen titulada Solve Math Problems Step 1$

1
Identifica el tipo de problema. ¿Es un problema de palabras, fracciones o de una ecuación cuadrática? Determina la categoría que se adecua mejor al problema de matemáticas antes de avanzar. Tomarte el tiempo para identificar el tipo de problema es esencial para encontrar la mejor forma de resolverlo. ^{[1]
X
Fuente de investigación}
$Imagen titulada Solve Math Problems Step 2$

2
Lee el problema con cuidado. Incluso si el problema parece simple, léelo con mucho cuidado. No solo eches un vistazo al problema y trates de resolverlo. Si el problema es complejo, quizás necesites volver a leer el problema muchas veces antes de comprenderlo por completo. Solo tómate un tiempo y no continúes hasta que tengas certeza de aquello que el problema te pide que hagas.^{[2]
X
Fuente de investigación}^{[3]
X
Fuente de investigación}
$Imagen titulada Solve Math Problems Step 3$

3
Parafrasea el problema. Para ayudarte a entender el problema al que te enfrentas, puede ser útil decirlo o escribirlo con tus propias palabras. Simplemente, puedes decirlo o escribirlo si te encuentras en una situación en la que no puedes decirlo en voz alta, como durante un examen. Contrasta lo que has dicho o escrito con el problema original para asegurarte de representar el problema con exactitud.^{[4]
X
Fuente de investigación}^{[5]
X
Fuente de investigación}
$Imagen titulada Solve Math Problems Step 4$

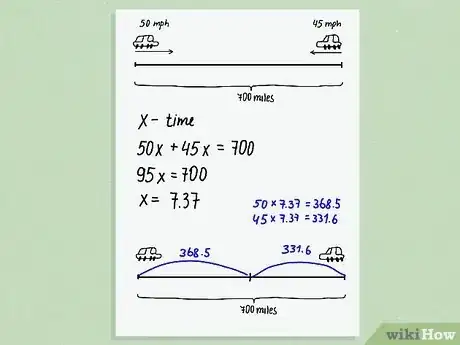
4
Dibuja el problema. Si crees que eso ayudará con el tipo de problema al que te enfrentas, crea una representación visual del problema para que te ayude a determinar lo que necesitas hacer después. El dibujo no tiene que ser elaborado, simplemente puede ser una forma o formas con números. Consulta el problema a medida que dibujes y contrasta el dibujo con el problema después de que termines. Pregúntate lo siguiente: “¿Mi dibujo representa el problema con exactitud?”. Si lo hace, entonces puedes continuar. En caso contrario, empieza de nuevo al volver a leer el problema.^{[6]
X
Fuente de investigación}^{[7]
X
Fuente de investigación}
- Dibuja un diagrama de Venn. Un diagrama de Venn muestra las relaciones entre los números en el problema. Los diagramas de Venn son muy útiles con los problemas de palabras.^{[8]
  X
  Fuente de investigación}
- Dibuja un gráfico o cuadro. ^{[9]
  X
  Fuente de investigación}
- Ordena los componentes del problema en una línea. ^{[10]
  X
  Fuente de investigación}
- Dibuja formas simples para representar las características más complejas del problema. ^{[11]
  X
  Fuente de investigación}
$Imagen titulada Solve Math Problems Step 5$

5
Busca patrones. A veces, simplemente puedes identificar un patrón o patrones en un problema de matemáticas al leerlo de forma meticulosa. También puedes crear una tabla para que te ayude a identificar un patrón o patrones en el problema. Anota cualquier patrón que identifiques en el problema. Estos pueden ayudarte a resolver el problema e incluso llevarte directamente a la respuesta.^{[12]
X
Fuente de investigación}
$Imagen titulada Solve Math Problems Step 6$

6
Revisa la información. Contrasta lo que has escrito con el problema para asegurarte de que hayas copiado los números y otra información con exactitud. No pases a la fase de planificación hasta que tengas certeza de que tienes toda la información requerida y que comprendas el problema por completo. Si no entiendes el problema, tómate un momento para ver algunos ejemplos en tu libro de texto o en línea. Ver la forma en la que otras personas han resuelto correctamente problemas similares puede ayudarte a comprender lo que este problema te pide que hagas.

Anuncio

Parte 2

Parte 2 de 3:
Desarrollar un plan

$Imagen titulada Solve Math Problems Step 7$

1
Determina las fórmulas que necesitarás para resolver el problema. Si el problema es particularmente complejo, quizás necesites más de una. Dedica un tiempo a revisar los conceptos en el libro de texto que te ayudarán a resolver el problema.^{[13]
X
Fuente de investigación}
$Imagen titulada Solve Math Problems Step 8$

2
Escribe lo que debes hacer para obtener la respuesta. Haz una lista paso a paso de las cosas que debes hacer para resolver el problema. Esta lista te ayudará a mantenerte organizado y concentrado a medida que resuelvas el problema. También puedes usarla para calcular la respuesta del problema antes de que realmente lo resuelvas.^{[14]
X
Fuente de investigación}^{[15]
X
Fuente de investigación}
$Imagen titulada Solve Math Problems Step 9$

3
Trabaja en un problema más fácil. Si hay un problema más fácil disponible que sea similar al que tratas de resolver, trabaja primero en él. Resolver un problema más fácil que requiere algunos de los mismos pasos y fórmulas te ayudará a abordar el problema más difícil.^{[16]
X
Fuente de investigación}^{[17]
X
Fuente de investigación}
$Imagen titulada Solve Math Problems Step 10$

4
Haz una deducción bien fundamentada sobre la respuesta. Trata de estimar la respuesta antes de realmente empezar a resolverlo. Identifica los números y los otros factores que deben contribuir con tu cálculo. Revisa el cálculo y la forma en la que lo hayas hecho para determinar si has olvidado incluir algo.^{[18]
X
Fuente de investigación}^{[19]
X
Fuente de investigación}

Anuncio

Parte 3

Parte 3 de 3:
Resolver el problema

$Imagen titulada Solve Math Problems Step 11$

1
Sigue el plan. Completa los pasos que has identificado en el orden en el que los has listado. Vuelve a revisar cada una de tus respuestas a medida que trabajes para garantizar la exactitud.^{[20]
X
Fuente de investigación}
$Imagen titulada Solve Math Problems Step 12$

2
Compara las respuestas con tus cálculos. A medida que completes cada paso, también puedes comparar las respuestas con los cálculos que hayas propuesto para cada paso y con el cálculo general de la respuesta del problema. Pregúntate lo siguiente: “¿Mis respuestas concuerdan o se parecen bastante a mis cálculos?”. Si no concuerdan, considera la razón. Revisa las respuestas para ver si has completado todos los pasos de forma correcta.^{[21]
X
Fuente de investigación}
$Imagen titulada Solve Math Problems Step 13$

3
Intenta un plan diferente. Si tu plan no funciona, regresa a la fase de planificación y elabora un nuevo plan. No te desanimes si esto sucede, los errores son comunes cuando recién estás aprendiendo a hacer algo, y aprenderás de ellos. Acepta los errores y continúa. Trata de no insistir en ellos ni de enojarte. ^{[22]
X
Fuente de investigación}
$Imagen titulada Solve Math Problems Step 14$

4
Reflexiona sobre el problema. Cuando hayas resuelto el problema de forma correcta, vuelve a ver el proceso. Tomarte un tiempo para reflexionar sobre el problema y en la forma en la que lo hayas resuelto te ayudará a enfrentar un problema similar la próxima vez. También te ayudará a identificar cualquier concepto que necesites para aprender más sobre eso y practicar. ^{[23]
X
Fuente de investigación}

Anuncio

Consejos

Busca la ayuda de tu profesor o tutor de matemáticas si te trabas o si has intentado varias estrategias sin éxito. Es probable que el profesor o tutor de matemáticas pueda identificar fácilmente lo que está mal y te ayude a comprender de qué forma corregirlo.

Anuncio

wikiHows relacionados

Anuncio

Referencias

Más referencias

Acerca de este wikiHow

Coescrito por:

Tutor académico

Este artículo fue coescrito por Daron Cam. Daron Cam es un tutor académico y el fundador de Bay Area Tutors, Inc., un servicio de tutorías con sede en el Área de la Bahía de San Francisco que brinda tutorías de matemáticas, ciencias y, sobre todo, el fomento de la confianza académica. Daron tiene más de 8 años enseñando matemáticas en las aulas y más de 9 años de experiencia en tutoría personalizada. Enseña todos los niveles de matemáticas, incluyendo cálculo, preálgebra, álgebra I, geometría y preparación de matemáticas para los exámenes SAT y ACT. Daron tiene una licenciatura de la Universidad de California, Berkeley, y una credencial de enseñanza de matemáticas otorgada por la St. Mary's College. Este artículo ha sido visto 18 912 veces.

Categorías: Carreras y educación

Anuncio