Feedforward neural network
A feedforward neural network (FNN) is an artificial neural network wherein connections between the nodes do not form a cycle.[1] As such, it is different from its descendant: recurrent neural networks.
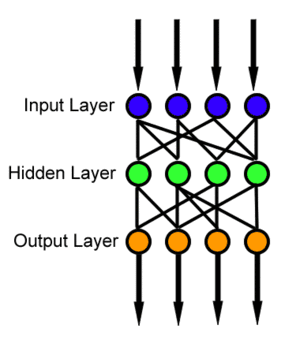
The feedforward neural network was the first and simplest type of artificial neural network devised.[2] In this network, the information moves in only one direction—forward—from the input nodes, through the hidden nodes (if any) and to the output nodes. There are no cycles or loops in the network.[1]
Linear neural network
The simplest kind of feedforward neural network is a linear network, which consists of a single layer of output nodes; the inputs are fed directly to the outputs via a series of weights. The sum of the products of the weights and the inputs is calculated in each node. The mean squared errors between these calculated outputs and a given target values are minimized by creating an adjustment to the weights. This technique has been known for over two centuries as the method of least squares or linear regression. It was used as a means of finding a good rough linear fit to a set of points by Legendre (1805) and Gauss (1795) for the prediction of planetary movement.[3][4][5][6][7]
Single-layer perceptron
The single-layer perceptron combines a linear neural network with a threshold function. If the output value is above some threshold (typically 0) the neuron fires and takes the activated value (typically 1); otherwise it takes the deactivated value (typically −1). Neurons with this kind of activation function are often called linear threshold units. In the literature the term perceptron often refers to networks consisting of just one of these units. Similar "neurons" were described in physics by Ernst Ising and Wilhelm Lenz for the Ising model in the 1920s,[8] and by Warren McCulloch and Walter Pitts in the 1940s.
A perceptron can be created using any values for the activated and deactivated states as long as the threshold value lies between the two.
Perceptrons can be trained by a simple learning algorithm that is usually called the delta rule. It calculates the errors between calculated output and sample output data, and uses this to create an adjustment to the weights, thus implementing a form of gradient descent.
Single-layer perceptrons are only capable of learning linearly separable patterns; in 1969 in a famous monograph titled Perceptrons, Marvin Minsky and Seymour Papert showed that it was impossible for a single-layer perceptron network to learn an XOR function. Nonetheless, it was known that multi-layer perceptrons (MLPs) are capable of producing any possible boolean function. For example, already in 1967, Shun'ichi Amari[9][6] trained an MLP by stochastic gradient descent.[10]
Although a single threshold unit is quite limited in its computational power, it has been shown that networks of parallel threshold units can approximate any continuous function from a compact interval of the real numbers into the interval [−1,1]. This result can be found in Peter Auer, Harald Burgsteiner and Wolfgang Maass "A learning rule for very simple universal approximators consisting of a single layer of perceptrons".[11]
A single-layer neural network can compute a continuous output instead of a step function. A common choice is the so-called logistic function:
With this choice, the single-layer network is identical to the logistic regression model, widely used in statistical modeling. The logistic function is one of the family of functions called sigmoid functions because their S-shaped graphs resemble the final-letter lower case of the Greek letter Sigma. It has a continuous derivative, which allows it to be used in backpropagation. This function is also preferred because its derivative is easily calculated:
(The fact that satisfies the differential equation above can easily be shown by applying the chain rule.)
If single-layer neural network activation function is modulo 1, then this network can solve XOR problem with a single neuron.
Multi-layer perceptron

This class of networks consists of multiple layers of computational units, usually interconnected in a feed-forward way. Each neuron in one layer has directed connections to the neurons of the subsequent layer. In many applications the units of these networks apply a sigmoid function as an activation function. However sigmoidal activation functions have very small derivative values outside a small range and do not work well in deep neural networks due to the vanishing gradient problem.
The universal approximation theorem for neural networks[12] states that every continuous function that maps intervals of real numbers to some output interval of real numbers can be approximated arbitrarily closely by a multi-layer perceptron with just one hidden layer. This result holds for a wide range of activation functions, e.g. for the sigmoidal functions.
Multi-layer networks use a variety of learning techniques. The first deep learning MLP was published by Alexey Grigorevich Ivakhnenko and Valentin Lapa in 1965.[13][14][6] They trained their MLP layer by layer, incrementally adding layers until the remaining error was acceptable, continually pruning superfluous hidden units with the help of a separate validation set.[6]
The first deep learning MLP trained by stochastic gradient descent[10] was published in 1967 by Shun'ichi Amari.[9] In computer experiments conducted by Amari's student Saito, a five layer MLP with two modifiable layers learned internal representations required to classify non-linearily separable pattern classes.[6]
Today, the most popular method for training MLPs is back-propagation. The terminology "back-propagating errors" was introduced in 1962 by Frank Rosenblatt,[15][6] but he did not know how to implement this, although Henry J. Kelley had a continuous precursor of backpropagation[16] already in 1960 in the context of control theory.[6] Modern backpropagation is actually Seppo Linnainmaa's general reverse mode of automatic differentiation (1970) for discrete connected networks of nested differentiable functions.[17][18] It is an efficient application of the chain rule (derived by Gottfried Wilhelm Leibniz in 1673[19][20]) to networks of differentiable nodes.[6] In 1982, Paul Werbos applied backpropagation to MLPs in the way that has become standard.[21][6] In 1985, David E. Rumelhart et al. published an experimental analysis of the technique.[22] Many improvements have been implemented in subsequent decades.[6]
During backpropagation, the output values are compared with the correct answer to compute the value of some predefined error-function. The error is then fed back through the network. Using this information, the algorithm adjusts the weights of each connection in order to reduce the value of the error function by some small amount. After repeating this process for a sufficiently large number of training cycles, the network will usually converge to some state where the error of the calculations is small. In this case, one would say that the network has learned a certain target function. To adjust weights properly, one applies a general method for non-linear optimization that is called gradient descent, due to Augustin-Louis Cauchy, who first suggested it in 1847.[23] For this, the network calculates the derivative of the error function with respect to the network weights, and changes the weights such that the error decreases (thus going downhill on the surface of the error function). For this reason, back-propagation can only be applied on networks with differentiable activation functions.
In general, the problem of teaching a network to perform well, even on samples that were not used as training samples, is a quite subtle issue that requires additional techniques. This is especially important for cases where only very limited numbers of training samples are available.[24] The danger is that the network overfits the training data and fails to capture the true statistical process generating the data. Computational learning theory is concerned with training classifiers on a limited amount of data. In the context of neural networks a simple heuristic, called early stopping, often ensures that the network will generalize well to examples not in the training set.
Other typical problems of the back-propagation algorithm are the speed of convergence and the possibility of ending up in a local minimum of the error function. Today, there are practical methods that make back-propagation in multi-layer perceptrons the tool of choice for many machine learning tasks.
One also can use a series of independent neural networks moderated by some intermediary, a similar behavior that happens in brain. These neurons can perform separably and handle a large task, and the results can be finally combined.[25]
Other feedforward networks
More generally, any directed acyclic graph may be used for a feedforward network, with some nodes (with no parents) designated as inputs, and some nodes (with no children) designated as outputs. These can be viewed as multilayer networks where some edges skip layers, either counting layers backwards from the outputs or forwards from the inputs. Various activation functions can be used, and there can be relations between weights, as in convolutional neural networks.
Examples of other feedforward networks include radial basis function networks, which use a different activation function.
Sometimes multi-layer perceptron is used loosely to refer to any feedforward neural network, while in other cases it is restricted to specific ones (e.g., with specific activation functions, or with fully connected layers, or trained by the perceptron algorithm).
References
- Zell, Andreas (1994). Simulation Neuronaler Netze [Simulation of Neural Networks] (in German) (1st ed.). Addison-Wesley. p. 73. ISBN 3-89319-554-8.
- Schmidhuber, Jürgen (2015-01-01). "Deep learning in neural networks: An overview". Neural Networks. 61: 85–117. arXiv:1404.7828. doi:10.1016/j.neunet.2014.09.003. ISSN 0893-6080. PMID 25462637. S2CID 11715509.
- Mansfield Merriman, "A List of Writings Relating to the Method of Least Squares"
- Stigler, Stephen M. (1981). "Gauss and the Invention of Least Squares". Ann. Stat. 9 (3): 465–474. doi:10.1214/aos/1176345451.
- Bretscher, Otto (1995). Linear Algebra With Applications (3rd ed.). Upper Saddle River, NJ: Prentice Hall.
- Schmidhuber, Juergen (2022). "Annotated History of Modern AI and Deep Learning". arXiv:2212.11279 [cs.NE].
- Stigler, Stephen M. (1986). The History of Statistics: The Measurement of Uncertainty before 1900. Cambridge: Harvard. ISBN 0-674-40340-1.
- Brush, Stephen G. (1967). "History of the Lenz-Ising Model". Reviews of Modern Physics. 39 (4): 883–893. Bibcode:1967RvMP...39..883B. doi:10.1103/RevModPhys.39.883.
- Amari, Shun'ichi (1967). "A theory of adaptive pattern classifier". IEEE Transactions. EC (16): 279–307.
- Robbins, H.; Monro, S. (1951). "A Stochastic Approximation Method". The Annals of Mathematical Statistics. 22 (3): 400. doi:10.1214/aoms/1177729586.
- Auer, Peter; Harald Burgsteiner; Wolfgang Maass (2008). "A learning rule for very simple universal approximators consisting of a single layer of perceptrons" (PDF). Neural Networks. 21 (5): 786–795. doi:10.1016/j.neunet.2007.12.036. PMID 18249524. Archived from the original (PDF) on 2011-07-06. Retrieved 2009-09-08.
- Cybenko, G. 1989. Approximation by superpositions of a sigmoidal function Mathematics of Control, Signals, and Systems, 2(4), 303–314.
- Ivakhnenko, A. G. (1973). Cybernetic Predicting Devices. CCM Information Corporation.
- Ivakhnenko, A. G.; Grigorʹevich Lapa, Valentin (1967). Cybernetics and forecasting techniques. American Elsevier Pub. Co.
- Rosenblatt, Frank (1962). Principles of Neurodynamics. Spartan, New York.
- Kelley, Henry J. (1960). "Gradient theory of optimal flight paths". ARS Journal. 30 (10): 947–954. doi:10.2514/8.5282.
- Linnainmaa, Seppo (1970). The representation of the cumulative rounding error of an algorithm as a Taylor expansion of the local rounding errors (Masters) (in Finnish). University of Helsinki. pp. 6–7.
- Linnainmaa, Seppo (1976). "Taylor expansion of the accumulated rounding error". BIT Numerical Mathematics. 16 (2): 146–160. doi:10.1007/bf01931367. S2CID 122357351.
- Leibniz, Gottfried Wilhelm Freiherr von (1920). The Early Mathematical Manuscripts of Leibniz: Translated from the Latin Texts Published by Carl Immanuel Gerhardt with Critical and Historical Notes (Leibniz published the chain rule in a 1676 memoir). Open court publishing Company.
- Rodríguez, Omar Hernández; López Fernández, Jorge M. (2010). "A Semiotic Reflection on the Didactics of the Chain Rule". The Mathematics Enthusiast. 7 (2): 321–332. doi:10.54870/1551-3440.1191. S2CID 29739148. Retrieved 2019-08-04.
- Werbos, Paul (1982). "Applications of advances in nonlinear sensitivity analysis" (PDF). System modeling and optimization. Springer. pp. 762–770. Archived (PDF) from the original on 14 April 2016. Retrieved 2 July 2017.
- Rumelhart, David E., Geoffrey E. Hinton, and R. J. Williams. "Learning Internal Representations by Error Propagation". David E. Rumelhart, James L. McClelland, and the PDP research group. (editors), Parallel distributed processing: Explorations in the microstructure of cognition, Volume 1: Foundation. MIT Press, 1986.
- Lemaréchal, C. (2012). "Cauchy and the Gradient Method" (PDF). Doc Math Extra: 251–254.
- Roman M. Balabin; Ravilya Z. Safieva; Ekaterina I. Lomakina (2007). "Comparison of linear and nonlinear calibration models based on near infrared (NIR) spectroscopy data for gasoline properties prediction". Chemometr Intell Lab. 88 (2): 183–188. doi:10.1016/j.chemolab.2007.04.006.
- Tahmasebi, Pejman; Hezarkhani, Ardeshir (21 January 2011). "Application of a Modular Feedforward Neural Network for Grade Estimation". Natural Resources Research. 20 (1): 25–32. doi:10.1007/s11053-011-9135-3. S2CID 45997840.