Número racional

Número racional
Concepto:Es aquel número que puede escribirse con la expresion a/b, donde a y b son enteros y b es distinto de 0.

Número racional. Es aquel que puede escribirse como donde y .
Como conjunto numérico se identifica con el símbolo .

Antecedentes históricos.

Aunque las cantidades fraccionarias habían sido representadas de disimiles formas en las distintas civilizaciones antiguas que tuvieron la necesidad de usarlas; es el matemático Fibonacci quien establece su forma de representación actual en el "Liber Abaci" de 1202.
Anteriormente, los egipcios por ejemplo para representar utilizaban la suma , pues solo tenían fracciones de numerador 1 o alícuotas. Para ello incluso habían ido refinando a lo largo del tiempo tablas de conversión en los que definían una serie de fracciones tipos y sus representaciones como suma de alícuotas.
De igual manera, hay registros del uso de fracciones en Babilonia, Grecia, China, India, Persia y otras civilizaciones, que además usaban sus versiones negativas antes de que los números negativos fueran de uso común en Occidente para el siglo XVII.

Representación.

Todo número racional puede escribirse en notación fraccionaria como donde y . Ejemplos: . 1 tiene por representación cualquier expresión para k entero distinto de 0. Un entero k no nulo se representa de la forma y el 0 puede expresarse como una fracción .

En el caso de que el número esté fuera del rango -1 a 1, ambos incluidos, puede usarse la notación mixta que es una convención para representar la suma n + f, donde n es un entero y f una fracción positiva entre 0 y 1. .

En notación decimal los racionales pueden reconocerse porque están escritos como mismo los enteros o por la presencia de un cantidad exacta de cifras tras la coma o por una secuencia de números que se repite infinitamente llamada período y se denota mejor con una línea encima de las cifras que conforman el período infinito .

Cambio de representación.

Evidentemente con toda esta variedad de notaciones tienen que existir formas de llevar de una a otra:

Notación Fracción Mixta Decimal
Fracción $



Si x>1 ó x<-1, se calcula la parte
entera y al lado se indica la fracción resto del mismo
denominador.		 Realizar la división hasta que sea exacta
o hasta hallar el periodo.
Mixta Multiplicar el valor entero por el denominador
y agregar el numerador. El resultado será
el nuevo numerador de la fracción
que conserva el mismo denominador.		 $ Realizar la división hasta que sea exacta
o hasta hallar el periodo,
anteponer el valor entero al resultado.

Simplificación de fracciones.

La representación fraccionaria tiene el inconveniente de que un mismo número racional puede aparecer descrito en varias fracciones, por lo que se han dispuesto varias formas de reducirlas a la forma en que el numerador y denominador no existan factores comunes. Una de ellas es el siguiente algoritmo:

  1. s = -1 si numerador*denominador negativo, 0 si numerador*denominador = 0, 1 si positivo
  2. n = módulo del numerador
  3. d = módulo del denominador
  4. i = 2
  5. Mientras i<=n e i<=d:
    1. Mientras n y d sean múltiplos de i:
      1. n = n/i
      2. d = d/i
    2. i = i+1
  6. fraccion = (s*n)/d

Al terminar la fracción queda en su expresión mínima, pues han sido eliminados todos los factores comunes.

Representación en el rayo numérico.

Los números racionales también pueden disponerse en la recta numérica según su valor en notación decimal para facilitar el posicionamiento. Por lo que a cada racional le pertenece un único lugar en la recta numérica.

Propiedades.

Los racionales incluyen al conjunto de los enteros, los Números fraccionarios (que son las fracciones positivas) y sus opuestos, las fracciones negativas. A su vez son subconjunto de los números reales.

En el conjunto de los racionales sus elementos soportan el ordenamiento, pues puede definirse entre dos números racionales distintos cuál es mayor que el otro, así como en cualquiera de sus representaciones puede verificarse si hay igualdad entre racionales.

Son un conjunto infinito ya que se cumple la propiedad de que entre cualquier par de racionales distintos x e y donde x<y, existe un número racional z tal que x<z<y.

El conjunto Q de todos los números racionales en numerable ; esto quiere decir que se puede establecer una biyección entre el Conjunto Q y el conjunto N de los naturales ( estrictamente enteros positivos)

Caracterización algebraica

El conjunto Q de los número racionales es grupo abeliano con la operación de la [[suma]|adiicíon] y el conjuntp Q0 con la multiplicación es también un grupo. Q con las dos operaciones es un cuerpo algebraico.. El 0 es el neutro de la suma. El 1 es la unidad para la multiplicación.
Para todo racional x su opuesto se obtiene mediante la negación -x, lo que implica en la notación fraccionaria cambiar el signo de la fracción por su opuesto. El inverso de un racional para el producto es siempre que .

Toda ecuación de primer grado con una incógnita tiene siempre una solución en el conjunto Q de los números racionales.

Caracterización topológica

El conjunto Q, con la topología relativa usual de los números reales se caracteriza por:

  • Si interior es el conjunto vacío {}.
  • Su clausura es el conjunto R de los números reales. Pues los números irracionales, son precisamente puntos de acumulación de números racionales; como en el caso de 21/2 es punto de acumulación del conjunto H de los números racionales racionales positivos, cuyo cuadrado es menor que 2.
  • Un número real está en la frontera del conjunto de los números racionales; pues todo número real x esta en un intervalo abierto <x-r; x+r> que contiene tanto números racionales y de su complemento , los números irracionales. [1]
  • Dados dos números racionales r y s siempre existe entre ellos otro racional; para el caso (r+s)/2. [2]

Operaciones. y relaciones

Con los los números racionales se pueden, irrestrictamente, las siguientes operaciones, salvo la división por cero.:

  • Comparaciones o relación de igual y de orden
    • =.
    • <.
    • >.
  • Aritmética.
    • Adición.
    • Substracción.
    • Multiplicación.
    • División.

Sean los racionales descritos en notación fraccionaria y con y se cumple:

Comparaciones.

  • Igualdad: .
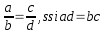
  • Menor que: .
  • Mayor que: .

Aritmética.

  • Adición:.
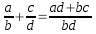
  • Sustracción:.
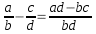
  • Multiplicación:.
  • División:. En este caso también .
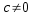
  • Potenciación: (a/b)n = an/bn donde n es entero no negativo.

Referencias

  1. ↑ M. J. Mansfield: Introducción a la topología. Editorial Alhambra, Madrid (1974) ISBN 84-205-0450-5
  2. ↑ Vicente Ampuero: Aritmética teórica

Fuentes.

  • Carl B. Allendoerfer, Cletus O. Oakley. Introducción moderna a la matemática superior. Ediciones del Castillo, Madrid. 1967.
  • K. Ríbnikov. Historia de las Matemáticas. Editorial MIR, Moscú. 1987.
  • Allendoerfer, Carl B. con Oakley, Cletus. Fundamentos de matemáticas universitarias. Mc Graw Hill, México, 1990, 3ra. edición, isbn 0-07-001366-7
This article is issued from Ecured. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.