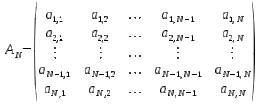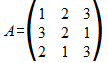Valor propio

Valor propio

Concepto:	Escalar k que satisface T(V)=kV donde V es un vector propio de T.

Valor propio. (Del alemán eigenvert traducido como autovector) Dícese del escalar k que en una aplicación lineal T multiplica al vector propio no nulo V de la forma T(V)=kV.

El termino eigenvert se atribuye al matemático David Hilbert en 1904.

Vectores y valores propios juegan un importante papel en la simplifación operatoria dentro de las transformaciones lineales al encontrar la matriz diagonal semejante a la matriz cuadrada asociada a dicha aplicación.

Definición

Sea T una aplicación o transformación lineal endomórfica de orden N, se dice que el escalar k es un valor propio si y sólo si existe el vector no nulo V tal que:

T(V)=kV

Propiedades

Los elementos de la diagonal principal de una matriz diagonal son propios.
Las raíces del polinomio característico de la matriz asociada a la transformación lineal son valores propios.
Las soluciones de la ecuación con determinante |A-kI|=0, donde A es la matriz cuadrada de orden N asociada al endomorfismo en cuestión e I es la matriz identidad de orden N, son valores propios.

Ejemplo

Sea la matriz A:

asociada a la aplicación lineal T:R³->R³; obtener los valores propios de A.

1ro. Se plantea |A-kI|=0 para obtener el polinomio característico:

que es reducido a:

-k³+6k²+2k-12=0 (Polinomio característico de A)

2do. Se determinan las raíces del polinomio:

-k³+2k+6k²-12=0
=-k(k²-2)+6(k²-2)
(6-k)(k²-2)=0

siendo 6 y que son valores propios de A.

Importancia

Los valores propios, junto a otras propiedades de las matrices cuadradas, son la clave para la diagonalización de matrices cuadradas por otras matrices diagonales semejantes. Una vez encontrada la matriz diagonal semejante, los cálculos de la aplicación lineal se simplifican notablemente a meros productos.

Este proceso de obtención de valores y vectores se realiza mediante la resolución del polinomio característico de la matriz cuadrada asociada a la transformación lineal en cuestión, usando por lo general el teorema de Cayley-Hamilton. Para matrices superiores al orden 3, se obtendrán polinomios que según el Teorema de Abel-Ruffini no tendrán un método genérico de descomposición.

Véase también

Fuentes

Colectivo de Autores. Álgebra lineal. Editorial Félix Valera. La Habana, 2003.
K. Ribnikov. Análisis Combinatorio. Editorial Mir, Moscú. 1988.
Valor propio en Wikipedia. Consultado el 4 de septiembre de 2017.

This article is issued from Ecured. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.