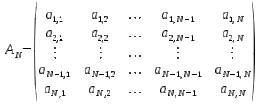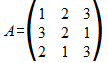Vector propio

Vector propio

Concepto:	Vector V que satisface T(V)=kV donde k es un valor propio de la transformación lineal T.

Vector propio. (Del alemán eigenvert traducido como autovector) Dícese del vector V que en una aplicación lineal T multiplica al valor propio no nulo k en la forma T(V)=kV.

El termino eigenvert se atribuye al matemático David Hilbert en 1904.

Vectores y valores propios juegan un rol medular en la simplifación operatoria (solo un producto por fila) dentro de las transformaciones lineales, al permitir hallar a la matriz diagonal semejante a la matriz cuadrada asociada a T.

Definición

Sea T una aplicación o transformación lineal endomórfica de orden N, se dice que el vector V no nulo es un vector propio si y sólo se transforma de la manera:

T(V)=kV

donde k es un valor propio.

Ejemplo

Sea la matriz A:

asociada a la aplicación lineal T:R³->R³; obtener los valores propios de A.

1ro. Se plantea |A-kI|=0 para obtener el polinomio característico:

que es reducido a:

-k³+6k²+2k-12=0 (Polinomio característico de A)

2do. Se determinan las raíces del polinomio:

-k³+2k+6k²-12=0
=-k(k²-2)+6(k²-2)
(6-k)(k²-2)=0

siendo 6 y que son valores propios de A por ser reales.

3ro. Se calculan los subespacios vectoriales de cada valor propio, sustituyéndolos por k en el sistema:

Para k=6 el subespacio vectorial es {(a,b,c)€R³ | a=b=c}.

Luego se determina un vector no nulo cualquiera por cada subespacio vectorial que serán vectores propios del correspondiente valor propio. En el caso del valor propio 6 puede un vector propio suyo sería (1,1,1).

Importancia

Los valores y vectores propios son clave para la diagonalización de matrices cuadradas, proceso que se hace mediante la resolución del polinomio característico de la matriz cuadrada asociada a la transformación lineal en cuestión, usando por lo general el teorema de Cayley-Hamilton. Una vez encontrada la matriz diagonal semejante, los cálculos de la aplicación lineal se simplifican notablemente a meros productos. Para matrices superiores al orden 3, se obtendrán polinomios que no tendrán un método general de factorización.

Véase también

Fuentes

Colectivo de Autores. Álgebra lineal. Editorial Félix Valera. La Habana, 2003.
K. Ribnikov. Análisis Combinatorio. Editorial Mir, Moscú. 1988.
Proskuriakov, I. Problemas de Álgebra Lineal. Editorial Mir, Moscú. 1986.
Valor propio en Wikipedia. Consultado el 4 de septiembre de 2017.

This article is issued from Ecured. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.