Anillo (álgebra)

Anillo algebraico
Concepto:Estructura algebraica de un conjunto no vacío y dos operaciones *, @ sobre éste cerradas y asociativas, * es conmutativa y en ella se verifica la existencia del neutro y los inversos para cada elemento del conjunto y juntas * y @ satisfacen la distributividad.

En álgebra, un Anillo es la estructura algebraica conformada por la terna <A,*,@>, donde A es un conjunto no vacío, * y @ son operaciones binarias; y se cumple estrictamente que * es cerrada, asociativa y conmutativa, sobre ella existe el elemento neutro y también los inversos de cada elemento de A. @ es cerrada y asociativa.@ es distributiva respecto a la operación * :Esto es: a@(b *c) = (a @ b) * (a @ c).

En el caso que <A,*,@> sea un anillo y @ sea conmutativa se dice que es un anillo conmutativo. Además, si existe el neutro sobre @ llamado elemento unidad se dice que <A,*,@> es un anillo conmutativo con elemento unidad.

Si <A,*,@> es un anillo y existe el elemento unidad para @ se está en presencia de un anillo con elemento unidad.

Definición

Sea un conjunto A no vacío y las operaciones binarias * y @ que satisfacen los siguientes axiomas:

  1. Clausura de *: . * es cerrada.
  2. Asociatividad de *: Para todos x, y, z de A, (x*y)*z=x*(y*z).
  3. Conmutitividad de *: Para todos x e y en A se cumple x*y=y*x.
  4. Existencia del neutro: Existe uno y solo un elemento e de A tal que para todo x de A se cumple que x*e=e*x=x. e es llamado neutro para * en A.
  5. Existencia de los inversos: Para todo x en A, existe un único elemento x" también en A, que satisface x*x"=x"*x=e. A x" se denomina inverso de x según *.
  6. Clausura de @: . * es cerrada.
  7. Asociatividad de @*: Para todos x, y, z de A, (x@y)@z=x@(y@z).
  8. Distributividad: Para todos x, y, z de A, x@(y*z)=x@y * x@z.

Se dice que A con las operaciones * y @ es un anillo.

El incumplimiento de cualquiera de los axiomas precedentes inhabilita la condición de anillo.

Apoyándose en otras definiciones del álgebra puede decirse que:

  • Sea A un conjunto no vacío con dos operaciones binarias * y @ es un anillo si y sólo si <A,*> es un grupo abeliano, <A,@> es un monoide y se satisface la ley distributiva x@(y*z)=(x@y)*(x@z) para todos x, y, z de A

Definición alternativa 1

Un conjunto S se denomina anillo, si se han definido sobre él dos operaciones , denominadas adición y multiplicación, siendo ambas conmutativas y asociativas, y vinculadas por la ley distributiva, conllevando además la adición la operación inversa, denominada resta. [1]

Definición alternativa 2

Sea el conjunto R un conjunto no vacío de diversa naturaleza, sea numérica, geométrica, matricial, aplicaciones, con dos operaciones algebraicas independientes, que se llamarán adición, denotada por + y multiplicación, indicada por yuxtaposición, si se cumple lo siguiente:

  1. El conjunto R con la adición es un grupo abeliano.
  2. El conjunto R con la multiplicación es un semigrupo
  3. L a multiplicacción es distributiva respecto de la adicióna(b + c) = ab + ac, (a + b)c = ac + bc,

El conjunto R que cumple las tres condiciones anteriormente señaladas se denomina anillo. R provisto de dos operaciones es un sistema algebraico más complejo que el grupo. [2]

Ejemplos

  1. Los números enteros son un anillo de la forma .
  2. Sea Mn el conjunto de las matrices cuadradas de orden n, puede decirse que es un anillo.
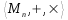
    1. Para todas las matrices cuadradas de n filas A y B A+B también es una matriz cuadrada de n filas y columnas.
    2. La suma de matrices cuadradas del mismo orden n es asociativa.
    3. La suma de matrices cuadradas del mismo orden n es conmutativa.
    4. es el neutro para la suma.
    5. Para toda matriz cuadrada de n filas y columnas se tiene su inverso dado por y según la suma de matrices .
    6. El producto de matrices cuadradas de orden n es cerrado.
    7. El producto de matrices cuadradas de orden n es asociativo.
    8. Para todas matrices cuadradas de orden n A, B, C se cumple A(B+C)=AB+AC.
  3. Todo cuerpo <C,*,@> es también un anillo.
  4. Por tanto los conjuntos numéricos racionales, reales y complejos que son cuerpos con la suma y la multiplicación también se constituyen en anillos sobre esas mismas operaciones.

Otros ejemplos

  • El conjunto P de los números enteros pares, provisto de las usuales operaciones de adición y multiplicación de números enteros es un anillo.
  • El conjunto de polinomios en la indeterminada x con coeficientes de un campo numérico prouesto, inclusive de un anillo numérico dado.
  • Tomemos el conjunto de las funciones , determinadas para todos los valores reales de t y que toman valores reales. En él se definen la suma de las funciones f(t) y h(t) será la función cuyo valor para cualquier t = t0 será igual a la suma de los valores de las funciones dadas, esto es, f(t0) +g(t0); el producto de estas funciones será una función cuyo valor para cualquie t = t0 será igual a f(t0) . g(t0). En este caso se puede comprobar que se cumplen los requisitos para ser anillo; la diferencia de funciones en t = t0 es la función cuyo valor es f(t0) - g(t0).

Fuentes

  • Carl B. Allendoerfer, Cletus O. Oakley. Introducción moderna a la matemática superior. Ediciones del Castillo, Madrid. 1967.

Referencias

  1. ↑ A.G. Kurosch. Curso de álgebra superior. Editorial Mir, Moscú (1981) Impreso en la URSS. Traducido del ruso por Emiliano APARICIO BERNARDO
  2. ↑ A. I. Kostrikin Introducción al álgebra Editorial Mir Moscú (1983)
This article is issued from Ecured. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.