Transformación de autómata finito no determinista con transición vacía a autómata finito no determinista

Transformación de AFND-V a AFND
Concepto:Algoritmo que permite encontrar a partir de un AFND-V un AFND estricto equivalente.

Transformación de autómata finito no determinista con transición vacía a autómata finito no determinista. Todo autómata finito no determinista con transición vacía, o sea AFND-V,, puede ser transformado a AFND utilizando un algoritmo basado en la clausura-xi que agrupa los estados sin transiciones significativas, dejando solo aquellas que reconocen símbolos del alfabeto del autómata, iterando cada vez así eliminar el indeterminismo por cadenas vacías.

Este algoritmo siempre obtiene un AFND equivalente al que pueden deben aplicarse otras transformaciones para obtener un AFD.

Algoritmo

Sea un autómata finito no determinista con transiciones vacías (AFND-V) definido por la 5-tupla A=<Q, T, g, F, q0>, donde Q es el conjunto de estados, T el alfabeto de símbolos terminales, g la relación de transiciones , F los estados finales, de llegada o aceptación y q0 es el estado inicial o de partida, el mismo puede transformarse en un autómata finito no determinista siguiendo los pasos:

  1. Se calcula A=clausura-ε(q0), siendo A un conjunto que corresponderá al estado inicial del nuevo autómata.
  2. Para cada símbolo del alfabeto, se verifican los estados alcanzables a partir de algún estado contenido en A, y se calcula la clausura-ε de dichos estados alcanzables. Si dichas clausuras producen nuevos conjuntos distintos de A, estos serán nuevos estados a los que se accederá a partir de A y del símbolo correspondiente.
  3. Se repite lo anterior para cada nuevo conjunto, hasta que no existan transiciones posibles para ningún símbolo del alfabeto.
  4. Los estados finales serán aquellos que contengan a antiguos estados finales.

Ejemplo

Dado el AF A=<{Q0,Q1,Q2,Q3,Q4,F1,F2},{a,b},{<Q0,chi,Q1>,<Q1,chi,Q2>,<Q1,chi,Q2>,<Q2,chi,F1>,<Q0,chi,Q3>,<Q3,a,Q4>,<Q4,b,F1>,<Q4,chi,F2>},{F1,F2},Q0> y su representación en diagrama de estados:

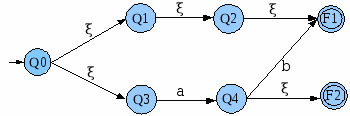
Obtener un AFND equivalente.

Las clausuras-xi de cada uno de sus estados serían:

  • clausura-ε(Q0)={Q0,Q1,Q2,F1,Q3}.
  • clausura-ε(Q1)={Q1,Q2,F1}.
  • clausura-ε(Q2)={Q2,F1}.
  • clausura-ε(F1)={F1}.
  • clausura-ε(Q3)={Q3}.
  • clausura-ε(Q4)={Q4,F2}.
  • clausura-ε(F2)={F2}.

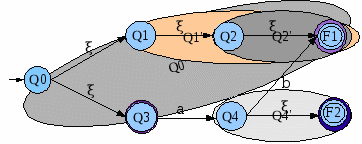
  1. Ahora se obtiene el estado inicial Q0*=clausura-ε(Q0)={Q0,Q1,Q2,F1,Q3}.
    1. Q0* solo tiene transiciones con el terminal a partiendo originalmente de Q3 hacia Q4, pero Q4*=clausura-ε(Q4))={Q4,F2}.
  2. Desde Q4* se puede tomar la transición no vacía <Q4,b,F1>, con F1*=clausura-ε(F1))={F1}.
  3. F1* no tiene transiciones.

Luego, el nuevo autómata finito no determinista sería A=<{Q0*,Q4*,F1*}, {a,b}, {<Q0*,a,Q4*>,<Q4*,b,F1*>}, {Q0*,Q4*,F1*}, Q0*> con una posible representación en diagrama de estados:

Consecuencias

La existencia de este método permite la conversión de cualquier AFND-V a un AFND equivalente, es decir la eliminación del indeterminismo por cadena vacía, obtenido comúnmente mediante el algoritmo de Thompson, al obtener un AFND-V a partir de una expresión regular.

Si se deseara obtener a partir del AFND resultante su equivalente determinista, deben realizarse un grupo de transformaciones que retiren las transiciones no deterministas del autómata.

Evidentemente en ninguno de los casos los autómatas finitos obtenidos deben considerarse los únicos que reconocen el lenguaje regular en cuestión.

Vease también

Fuentes

  1. Tanembaum, A. Compilers: Principles, Tecniques, and Tools. Tomo 1. ACM Press. 5ta Edición.
  2. Conferencias de la Asignatura "Compilación 1" del Departamento de Ciencias de la Computación de la Universidad de Oriente. Santiago de Cuba, 2000.
  3. Autómata finito en Wikipedia. Consultado el 25 de noviembre de 2013.
  4. Acevedo Martínez, Liesner; Osorio Ramírez, Karel. Manual de apoyo a la docencia. Técnicas de Compilación: Manual Práctico para estudiantes de Informática. Libro electrónico en PDF. UCI. La Habana, 2011.
This article is issued from Ecured. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.