Transformación de autómata finito no determinista a autómata finito determinista

Transformación de AFND a AFD

Concepto:	Algoritmo que permite encontrar a partir de un AFND un AFD equivalente.

Transformación de autómata finito no determinista a autómata finito determinista. Todo AFND estricto, o sea un AFND que no es AFND-V, puede ser transformado a AFD utilizando un algoritmo que transforma los estados del AFND en nuevos estados que son subconjuntos de los estados originales y aplica a los mismos la clausura para confirmar la conexidad entre cada uno de los componentes y así eliminar el indeterminismo.

Este algoritmo aunque siempre obtiene un AFD equivalente no puede decirse que sea la versión minimal del mismo, para ello deben aplicarse otras transformaciones.

Algoritmo

Sea un autómata finito estrictamente no determinista (AFND) definido por la 5-tupla A=<Q, T, g, F, q₀>, donde Q es el conjunto de estados, T el alfabeto de símbolos terminales, la relación de transiciones ó (léase: del estado q_i mediante el terminal x se va a q_j), F son los estados finales o de llegada dentro de Q, q₀ es el estado inicial o de partida

A se transforma en A_AFD=<Q_A,T, g_A,F_A,q_0A>', tal que:
1. V_A=P(V)-{{}}, con P(V) que es el conjunto potencia de los vértices de A.
2. F_A={x | }.
3. g_A={<r,x,q> | }.
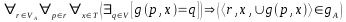
4. q_0A={q₀}.
Luego se eliminan de A_AFD todos los estados y sus correspondientes transiciones inalcanzables desde el estado inicial q_0A.

Ejemplo

Véase el proceso de transformación de AFND a AFD del autómata A=<{q0,q1,f},{a,b},{<q0,a,q0>,<q0,b,q0>,<q0,a,q1>,<q1,b,f>},{f},q0>, que reconoce a las cadenas de as y bs que comienzan con cualquiera cantidad de estas letras y terminan forzosamente en ab. El siguiente puede ser su diagrama de estados:

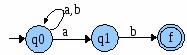
Primero se obtiene autómata derivado A_AFD=<V_AFD,T_AFD,g_AFD,F_AFD,{q0}> a partir del conjunto potencia de los estados de A donde:

V_AFD={{q0},{q1},{f},{q0,q1},{q0,f},{q1,f}, {q0,q1,f}}.
T_AFD={a,b}.
F_AFD={{f},{q0,f},{q1,f}, {q0,q1,f}}.

Cuyo diagrama sería:

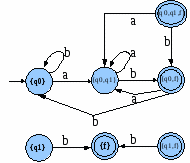
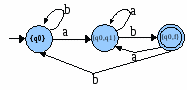
Luego se retiran los estados inaccesibles {q1}, {f}, {q1,f}, {q0,q1,f}, determinados mediante la clausura de {q0}, y queda:

A_AFD={{q0,{q0,q1},{q0,f}},{a,b},{<{q0},b,{q0}>,<{q0},a,{q0,q1}>,<{q0,q1},a,{q0,q1}>,<{q0,q1},b,{q0,f}>,<{q0,f},a,{q0,q1}>,<{q0,f},b,{q0}>},{ {q0,f} },{q0}}.

Consecuencias

La existencia de este método permite la conversión de cualquier AFND a un AFD equivalente, es decir la eliminación del indeterminismo estricto (el mismo símbolo terminal conduce a más de un estado desde un origen común), aunque no garantiza que sea el AFD equivalente minimal. Para ello deben seguirse otros pasos de reducción del AF.

Otra situación pudiera darse en el caso que se desee, por ejemplo, a partir de una expresión regular se desee obtener su autómata finito determinista, mediante el algoritmo de Thompson se obtiene el AFND-V, luego se procede por el método de la clausura-xi a su conversión a AFND y entonces puede aplicársele al autómata la transformación a AFD.

Vease también

Fuentes

Tanembaum, A. Compilers: Principles, Tecniques, and Tools. Tomo 1. ACM Press. 5ta Edición.
Conferencias de la Asignatura "Compilación 1" del Departamento de Ciencias de la Computación de la Universidad de Oriente. Santiago de Cuba, 2000.
Autómata finito en Wikipedia. Consultado el 25 de noviembre de 2013.
Acevedo Martínez, Liesner; Osorio Ramírez, Karel. Manual de apoyo a la docencia. Técnicas de Compilación: Manual Práctico para estudiantes de Informática. Libro electrónico en PDF. UCI. La Habana, 2011.

This article is issued from Ecured. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.